Scalar Product of Vectors

Properties of vectors

1) the vector collinear with the vector

2) ↑↑↑↑

3) =

4) = -

5) Given: the coordinate system

the vector modulus = 5

= 12

Find: OA

Solution:

OA== 13

OA = = 13

Answer: OA = 13

***

 

Let and be the given vectors.

1) From the point O we draw the vectors = and =

2) If ↑↓- are oppositely directed vectors, we see that the rays OA and OB form an angle AOB

3) If ↑↑- are co-directional vectors, we see that the angle between the vectors and is equal to 0°.

The angle between two vectors and is designated as:

 

Definition:

Two vectors are called perpendicular if the angle between them is 90°.

***

 

Problem 86.

Given:

ABCD - is the square

AC ∩ BD = O

 

Find: the angles between the vectors BAC, DAB = ?

Calculation:

a) Since AC - is the diagonal of the square, we see that it divides the angle A in half. Then the angle between the vectors = 45°

b) Since ABCD - is a square, we see that the degree measure of the angle between the vectors = = 90°, i.e. right angle.

***

 

Inner product of vectors

Problem 87.

Given:

ABCD - is the rhombus

BD = AB; AC ∩ BD = 0

 

Compute: the angle formed by the vectors

and , and , and = ?

Solution:

a) By the definition of the rhombus ΔABD - is equilateral (AB = AD = BD).

Hence, all the angles in the triangle are equal to 60°. Then the angle between the vectors = 60°

b) Since the vectors ↑↑are co-directional, the angle between the vectors = 0°

c) Since the vectors ↑↓ - are oppositely directed, we see that the angle between the vectors = 180°

***

 

Definition:

A scalar product of two vectors (formula 1) is the product of the lengths of these vectors by the cosine of the angle between them.

Designation: or

= *cos (a,b)     (1)

From the formula of the scalar product of vectors having used the cosine of the angle (1) it follows that:

1) the scalar product of vectors is greater than zero if the angle between vectors is less than 90°, i.e.

>0 if <90°

the scalar product of the vectors is less than zero if the angle between the vectors is greater than 90°, i.e.

<0 if >90°

2) If ↑↑ are co-directional vectors, we see that the angle between the vectors is equal to zero degrees, i.e. =0° =

3) If are the perpendicular vectors and =90° Cos 90° = 0, then = 0

The converse is also true, i.e. if = 0

Conclusion: = 0

***

 

Problem 88.

Given:

the vectors

=2

=3

the angle α = 90°

Find: scalar product of vectors

Solution:

Using the formula of the scalar multiplication of vectors by the cosine of the angle, we obtain

= •• Cos 90° = 2 • 3 • 0 = 0

Answer: = 0

***

 

Scalar Square

***

 

Problem 89.

Given:

the triangle ΔABC is equilateral

AB = a

 

Find: scalar product of vectors 1) 2)

Solution: In an equilateral triangle, all angles are equal to 60°.

1) = •Cos () = • =

2) = •Cos (120°) = -

***

 

Problem 90.

Given:

the vectors

=2; =3

1) the angle α = 45°

2) α = 135°

 

Find: scalar or inner product of vectors

Solution:

1) = •Cos 45° = 2 • 3 • = 3

2) = •Cos 135° = 2 • 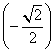3 • = -3

Answer: 1) 3; 2) -3

***

 

Problem 91.

Given:

the triangle ΔABC is equilateral

AB = a

the height BD

 

Find: scalar multiplication of vectors

1)

2) 3)

Solution:

1) = •Cos 120° = • (-Cos 60°) = -

2) since the vectors are perpendicular BDAC = 0

3) = =

Answer:1) -; 2) 0 ; 3)

 

Problem 92.

Given:

the figure ABCD is the rhombus

BD ∩ AC = 0

BD = AB

1) ;

2) ;

 

Find: the value of the angle between the vectors

1) ; 2)

Solution:

1) Consider the triangle ΔABC. This trianle is isosceles, since AB=BD.

Knowing that in the rhombus all sides are equal, we get ΔABD - is equilateral.

Then DAB =BDA = 60°

By the property of the rhombus it follows that ADC = 120°

Then the angle between the vectors =120°

 

2) Since the sides are parallel and the vectors are co-directed:

BA || CD and ↑↑ , then the vectors are parallel ||, therefore the vectors are equal =.

Consider a triangle ΔCBD is isosceles, since the two sides are equal: BD=BC.

By the definition of the rhombus, the triangle ΔCBD - is equilateral.

Hence, the angle BDC = 60°

By the property of the rhombus, the angle ADC = 120°.

Then the angle between the vectors is =120°.

Answer: 1) =120°; 2) =120°.

***

 

Scalar product of vectors in the Cartesian coordinate plane

Theorem:

If two vectors have coordinates {x₁; y₁}; { x₂; y₂}, then the scalar product of two vectors (formula 2) is the product of their coordinates:

(2)

 

Proof:

Case 1.

If any vector is equal to zero, then the equality (2) is obviously satisfied.

Case 2.

If the vectors and - are noncollinear.

We draw the vectors from an arbitrary point O.

Consider the triangle ΔOBA.

It is known that the cosine formula

c² = a² + b² - 2ab • Cos α, we obtain the equality

AB² = OB² + OA² - 2 • OB • OA • Cos α (3)

Using the values (*) = ; = ; = ; and also OA = ||; OB = || ; AB = ||, substituting the values of (*) in the equality (3), we obtain

||² = ||² + ||² - 2 (4)

Using the formula to calculate the length of the vector having used its coordinates, we obtain

=; =.

Since = {x₂ - x₁; y₂ – y₁}, then using the formula to calculate the distance between two points

, we obtain

|| = .

Then it follows from the equality (4) that

(x₂ - x₁)² + (y₂ – y₁)² = x₂² + y₂² + x₁² + y₁² - 2

x₂² -2 x₂ x₁ + x₁² + y₂² – 2 y₂y₁ + y₁² = x₂² + y₂² + x₁² + y₁² - 2

-2 x₂ x₁– 2 y₂y₁ = - 2

= x₂ x₁ + y₂ y₁

***

 

Consequences:

1) If the vectors are perpendicular, i.e.

{x₁; y₁}{ x₂; y₂} x₁ x₂ + y₁ y₂ = 0

2) By the definition of the scalar or inner product of two vectors (formula 1)

= •• Cos α

Cos α =

The formula to calculate the cosine of the angle having used the coordinates of the vectors:

 

To calculate the sine and the tangent of the angle between vectors by the cosine of an angle it’s used the reduction formulas and trigonometric functions.

 

***

 

The scalar vector multiplication

Problem 93.

If {; -1}; {2; 3}, then = 0.5 + (-3) = -2.5

***

 

Problem 94.

If {x; -1}; {3; 2} and the vectors are perpendicular , then = 3x - 2 0 = 3x - 2 2 = 3x x =

***

 

Problem 95.

Given:

the coordinates of the points

A(2;8), B(-1;5), C(3;1)

 

Find: the cosine of the angle between the vectors Cos A = ?

Solution:

Since each coordinate of the vector is equal to the difference of the corresponding coordinates of its end and the beginning

{b₁ – a₁; b₂ – a₂}, then

= {} = {}

= {} = {}

Using the formula to find the angles having used the coordinates of the vectors

Cos A =, we get

Cos A = ===

Answer: Cos A =

***

 

The length or the magnitude of a vector

Problem 96.

Given:

the angle between the vectors is equal to = =60° ,

magnitudes or lengths of vectors || = 1, || = || = 2

 

Find: the product of vectors ()= ?

Solution:

()=+= ||•||•Cos 60° + ||•||•Cos 60° = 1 + 2 = 3

Answer: ()= 3

***

 

Problem 97.

Given:

=, =

the magnitude or the length of the vectors ||=||=1

- are perpendicular vectors

Find: product of vectors = ?

Solution:

= ()•() = 3² + 12 - 2- 8² =

= 3² + 10 - 8² = 3||² + 0 - 8||² = -5.

Answer: = -5.

***

 

Problem 98.

Given:

{1.5 ; 2}, {4 ; -0.5}

 

Find: multiplication of vectors = ?

Solution:

= x₁ x₂ + y₁ y₂ = 6 + (-1) = 5

Answer: = 5.

***

 

Problem 99.

Given:

{0 ; -3}, {5 ; x}

are perpendicular vectors

 

Find: multiplication or product of vectors = ?

Solution:

= x₁ x₂ + y₁ y₂

0 = 0 + (-3x)

3x = 0

x = 0

Answer: under x=0, .

***

 

Problem 100.

Given:

the coordinates of the points

A(2;8), B(-1;5), C(3;1)

 

Find: the cosine of the angle of vectors

1) Cos B = ?

2) Cos C = ?

Solution:

1)

Since each coordinate of the vector is equal to the difference of the corresponding coordinates of its end and the beginning

{b₁ – a₁; b₂ – a₂}, then

= {} = {}

= {} = {}

Using the formula to find the angles having used the given vector coordinates

Cos B = , we get

Cos B = == 0

2)

= {} = {}

= {} = {}

Cos C = ===

Answer: Cos B =0, Cos C =

***

 

Problem 101.

Given:

, where i and j are coordinate vectors

 

Find: the length or the magnitude of the vector || = ?

Solution:

Let us find the coordinates of the vector .

{3; -4}

Since the length of the vector is equal to the square root of the sum of the squares of its coordinates || = , then we get

|| = = = 5.

Answer: || = 5.

***

 

Problem 102.

Given:

ABCD is the rhombus

AB =, AD =

 

Prove: the diagonals of the rhombus at the intersection point are perpendicular

ACBD or =0

Proof:

Since the figure ABCD is the rhombus and the parallelogram, then the vectors of the parallelogram ,

= -

= (+) (-) = - ² + ² - = ² -² = =||² -||² = 0. Therefore, the angle between the vectors = 90°. Hence, the diagonals of the rhombus at the intersection point are perpendicular, i.e. ACBD.

***

 

Problem 103.

Given:

the triangle ΔABC - is isosceles

AM is the median

 

Prove:

1) 4AM² = AB² + AC² + 2AB • AC • Cos A

2) CH = AM

Proof:

1) Since the point M is the midpoint of the side BC, we see that

2=

Therefore, (2) • (2) = ()() =

= AB² + 2AB + 2AB • AC • Cos A + AC² = AB² + AC² + 2AB • AC • Cos A

We get 4AM² = AB² + AC² + 2AB • AC • Cos A

 

2) By the formula obtained above, it follows that

4CH² = AC² + BC² + 2AC • BC • Cos C

Since the triangle ΔABC is isosceles, we see that AB = BC, A = C Cos A = Cos C

We get that 4CH² = AC² + BC²(=AB²) + 2AC • BC(=AB) • Cos C (= Cos A)

4CH² = AC² + AB² + 2AC • AB • Cos A

4CH² = 4AM²

=

2CH = 2AM | : 2

CH = AM

***

 

Problem 104.

Given:

ABCD is the convex quadrilateral

BD = d₁ and AC = d₂ are the diagonals

d₁ ∩ d₂ = O is the intersection point of the diagonals

 

Prove:

The area of the quadrilateral is equal to half the product of the diagonals by the sine of the acute angle between them

S_ABCD= d₁ • d₂ • Sin α

Proof:

The area of a quadrilateral is the sum of the areas of four triangles.

S_ABCD= S₁ + S₂ + S₃ + S₄ , where

S₁ = S_ΔAOB ; S₂ = S_ΔCOB ; S₃ = S_ΔCOD ; S₄ = S_ΔAOD

S₁ = BO • OA • Sin α

S₂ = BO • OC • Sin (180° - α) = BO • OC • Sin α

S₃ = CO • OD • Sin α

S₄ = AO • OD • Sin (180° - α) = AO • OD • Sin α

Adding S₁ + S₂ + S₃ + S₄, we obtain

S_ABCD= BO • Sin α (OA+OC) +

+ OD • Sin α (CO+OA)

Since OA+OC = AC, CO+OA = AC, BO + OD = BD we see that

S_ABCD=BO • AC • Sin α +OD • AC • Sin α =BD • AC • Sin α

 

The formula of the area of a convex quadrilateral:

S_ABCD= d₁ • d₂ • Sin α

 

 

***

 

Problem 105.

Given:

two vectors form an angle α = 150°,

the magnitudes or the lengths of vectors || = 2 , || = 2

 

Find: the length of the vector |2-| = ?

Solution:

BC² = AB² + AC² - 2 AB • AC • Cos 150°

BC² = 48 + 4 - 2 • 4• 2 • (-) = 52 + 24 = 76

BC = = 2

Answer: BC = |2-| = 2

***

 

Problem 106.

Given:

the triangle ΔABC

The angles B = 45°, C = 70°

a=24.6

 

Find: A - the angle in degrees, the sides b, c

Solution:

A = 180° - (45° + 70°) = 75°

 

Using the law of sines

, we obtain the expression

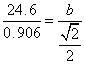
b = ≈ 19.2

c = ≈

≈ 25.5

Answer: A = 75°; b ≈ 19.2; c ≈ 25.5.

***

 

Problem 107.

Given:

the lengths of vectors || = 5, || = 8,

the angle between 2 vectors =60°

 

Find: the value of vectors

1) ||= ?

2) ||= ?

Solution: by the law of cosines

1)

AC² = AB² + BC² - 2AB • BC • Cos 120°

AC² = 25 + 64 - 80 • (- 0.5) = 129

AC = ±, but AC = - does not satisfy the solution of the problem. Therefore, AC =.

 

2) BC² = AB² + AC² - 2AB • AC • Cos 60°

BC² = 89 - 80 • 0.5 = 49

BC = ±, but BC = - 7 does not satisfy the solution of the problem. Therefore, BC = 7.

Answer: || =; || = 7.

***