The contents of this webpage:
Definition of a regular polygon:
The regular polygon is a convex polygon if the following conditions hold: the angles and the sides of this polygon are equal to each other. The examples of the regular polygon are a square, and an equilateral triangle.
Theorem - Derivation of the formula for calculating the angles of a regular polygon.
Given:
the regular polygon,
the angles α1, α2, α3, α4 ...
Prove:
αn = ![]() • 180°
• 180°
Proof:
The sum of the angles of this regular polygon (n - 2) • 180°.
By the condition α1 = α2 = α3 = α4 = ...![]()
each angle is ![]() • 180°, i.e. true is
• 180°, i.e. true is
the formula for calculating the angles of a regular polygon:
αn = ![]() • 180°
• 180°
***
Given: the regular hexagon, i.e. n = 6
Find: the angle of the regular hexagon
Solution:
αn = ![]() • 180° =
• 180° = ![]() = 120°
= 120°
Answer: 120°
***
Given: the regular polygon, where n is the number of sides of the polygon
Find: n - how many sides are contained in the regular polygon
Solution:
| 1) αn = 60° αn = 60° •n = (n - 2) • 180° 60° •n = 180°•n - 360° - 120° • n = - 360° n = 3 | 2) Since the angle of the regular polygon αn = 135° 135° •n = (n - 2) • 180° 135° •n - 180°•n = - 360° n = 8
|
***

ABCDEF is the regular polygon,
external angles β1; β2; ... ; βn
Find:
the sum of the external angles β1 + β2 + ... + βn = ?
Solution:
Since the hexagon is regular, then by definition of a regular polygon
each angle in the regular polygon is αn = ![]() • 180°
• 180°
αn = ![]() • 180° = 120°
• 180° = 120°
Since the all angles in the regular polygon are equal, then the external angles will also be equal, namely β1 = β2 = β3 = β4 = β5 = β6 = 180° -![]() FAB = 180° - 120° = 60°
FAB = 180° - 120° = 60°
Then β1 + β2 + β3 + β4 + β5 + β6 = 60° • 6 = 360°.
***
Given:
the regular polygon,
| 1) the regular triangle, n = 3 | 2) n = 5 | 3) n = 18 |
Find: the angle of the regular polygon
Solution:
| 1) αn = 3 • αn = 180° αn = 60° | 2) 5 • αn = 3 • 180° αn = 108° |
3) 18 • αn = 16 • 180° αn = 160° |
Answer: every angle of a regular polygon is 1) 60°; 2) 108°; 3) 160°.
***
Given:
the regular polygon,
αn = 90°
Determine: how many sides does the regular polygon have, i.e. n = ?
Solution:
αn = ![]() • 180°
• 180°
90° •n = (n - 2) • 180°
90° •n - 180°•n = - 360°
-90° •n = - 360°
n = 4
Answer: the number of sides of the regular polygon n = 4.
***
Definition:
A polygon is termed inscribed in a circle if all its vertices lie on a common circle.
Theorem:
About the regular polygon, it is possible to circumscribe a circle and, moreover, only one.

Given:
A1A2A3...An is the regular polygon
Prove:
there exists a unique circle of center at O and radius R such that the vertices of the regular polygon lie on this circle
![]() ! circle (O; R): A1; A2; A3;...An
! circle (O; R): A1; A2; A3;...An ![]() circle (O; R)
circle (O; R)
Proof:
1) We draw bisectors of the angle A1 and the angle A2.
Since the polygon is regular, we see that ![]() A1 =
A1 = ![]() A2
A2 ![]()
![]() 1 =
1 =![]() 2 =
2 =![]() 3 =
3 =![]() 4.
4.
From the condition ![]() 1 =
1 =![]() 3 it follows that the triangle ΔA1OA2 - is isosceles, so A1O = OA2
3 it follows that the triangle ΔA1OA2 - is isosceles, so A1O = OA2
Consider the triangle ΔA2OA3:
1) A2O - common side
2) A1A2 = A2A3
3) ![]() 3 =
3 =![]() 4
4
Then, by the first theorem of the equality of the triangles
Δ A1OA2 = Δ A2OA3. Therefore, A2O = A3O.
By connecting each remaining vertex to the point O, it can be shown that all the triangles are equal.
Then A1O =A2O = A3O = ... = AnO
Since the point O is the center of the circle and the radius is R = A1O =A2O = A3O = ... = AnO , we see that,
![]() ! circle (O; R): A1; A2; A3;...An
! circle (O; R): A1; A2; A3;...An ![]() circle (O; R)
circle (O; R)
Uniqueness:
Take any three vertices of the regular polygon; they form a triangle such that only one circle can be circumscribed about this triangle, it follows that only one circle can be circumscribed about the given polygon.

Given:
the regular polygon,
the arc AB= 60° (![]() AB = 60°)
AB = 60°)
AB is the side of the regular polygon
Find:
number of sides of the regular polygon, i.e. n = ?
Solution:
Since the degree measure ![]() AB = 60° < 180°, then the arc is equal to the angle, i.e.
AB = 60° < 180°, then the arc is equal to the angle, i.e.
![]() AB =
AB = ![]() AOB.
AOB.
ΔAOB - is isosceles, where ![]() OAB =
OAB = ![]() OBA =
OBA =
= (180° - 60°) : 2 = 60°.
Then ΔAOB is equilateral.
The radii of a circle circumscribed about the regular polygon are the bisectors of its angles, so each angle of the polygon is 60° • 2 = 120°.
Knowing that
αn = ![]() • 180°
• 180°
120° •n = (n - 2) • 180°
120° •n - 180°•n = - 360°
-60° •n = - 360°
n = 6
Answer: the number of sides of the regular polygon is n = 6.
***
Given:
the regular polygon,
| 1) | 2) |

AB is the side of the regular polygon
Find:
the number of sides of the polygon, i.e. n = ?
Solution:
1)
Since the degree measure ![]() AB = 36° < 180°, we see that the arc is equal to the angle, i.e.
AB = 36° < 180°, we see that the arc is equal to the angle, i.e.
![]() AB =
AB = ![]() AOB.
AOB.
ΔAOB is isosceles, where ![]() OAB =
OAB = ![]() OBA =
OBA =
= (180° - 36°) : 2 = 72°.
The radii of the circle circumscribed about the polygon are the bisectors of its angles, so each angle of the polygon is 72° • 2 = 144°.
Knowing that
αn = ![]() • 180°
• 180°
144° •n = (n - 2) • 180°
144° •n - 180°•n = - 360°
-36° •n = - 360°
n = 10
2)
Since the degree measure ![]() AB = 18° < 180°, then the arc is equal to the angle, i.e.
AB = 18° < 180°, then the arc is equal to the angle, i.e.
![]() AB =
AB = ![]() AOB, where the angle
AOB, where the angle ![]() AOB is central.
AOB is central.
ΔAOB is isosceles (OA = OB = r), where ![]() OAB =
OAB =
=![]() OBA = (180° - 18°) : 2 = 81°.
OBA = (180° - 18°) : 2 = 81°.
The radii of the circle circumscribed about the polygon are the bisectors of its angles, so each angle of the polygon is 81° • 2 = 162°.
Knowing that
αn = ![]() • 180°
• 180°
162° •n = (n - 2) • 180°
162° •n - 180°•n = - 360°
-18° •n = - 360°
n = 20
Answer: 1) n = 10; 2) n = 20.
***
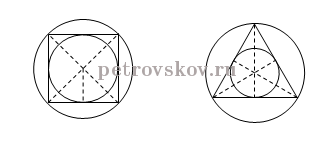
Conclusion:
In regular polygons, the centers of the inscribed and circumscribed circles coincide.
Given:
A1A2A3A4A5 is the regular pentagon

Prove:
A1A3 = A1A4
Proof:
By the definition of the regular polygon in a given pentagon, all sides and angles are equal.
Consider the triangles ΔA1A2A3 and ΔA1A4A5.
A1A2 = A1A5
A2A3 = A5A4
![]() A2 =
A2 =![]() A5
A5
Then, according to the first theorem of the equality of the triangles (ΔA1A2A3 = ΔA1A4A5) it follows that A1A3 = A1A4 as the corresponding sides.
***
Given:
ABCD is the square

AM : MK : KD = 1 : ![]() : 1
: 1
Prove:
MNOZLFEK is the regular polygon
Proof:
ΔAMN = ΔOBZ = ΔLCF = ΔEKD (by the first theorem of the equality of the triangles)
By the Pythagorean theorem:
MN = OZ = LF = EK = ![]()
By the condition NO = ZL = EF = MK = ![]()
Therefore, all sides are equal.
Since ![]() 1=
1=![]() 2 = 45°, then
2 = 45°, then ![]() NMK=
NMK=![]() MKE =
MKE = ![]() KEF=
KEF=![]() EFL =
EFL = ![]() FLZ=
FLZ=![]() ZON = ... = 180° - 45° = 135°
ZON = ... = 180° - 45° = 135°
It follows that MNOZLFEK is the regular octagon.
***
Theorem:
In any regular polygon, it is possible to inscribe a circle, and moreover only one.

Given:
A1A2A3...An is the regular polygon
Prove:
There is a unique inscribed circle of center at O and radius R
![]() ! circle (O; R): H1; H2; H3;...Hn
! circle (O; R): H1; H2; H3;...Hn ![]() circle (O; R)
circle (O; R)
Proof:
1) We draw the heights of the triangles, i.e. OH1; OH2; ...; OHn
It is known that the triangles are equal, i.e. ΔOA1A2 = ΔOA2A3 = ... = ΔOAnA1.
Therefore, OH1 = OH2 = ... = OHn . Then H1; H2; H3;...Hn ![]() circle (O; R).
circle (O; R).
Uniqueness:
2) Let us suppose that as well as the circle (O; R) there is another circle inscribed in a given polygon.
Then its center O1 is equidistant from the sides of the polygon and coincides with the point O of the intersection of the bisectrixes lying on each angle of the polygon.
Therefore, the radius of this circle is equal to OH1 and from this it follows that the circles coincide.
***

the regular polygon,
the arc AB= 72° (![]() AB = 72°)
AB = 72°)
AB is the side of the regular polygon
Find:
the number of sides of the polygon, i.e. n = ?
Solution:
Since the degree measure ![]() AB = 72° < 180°, then the arc is equal to the angle, i.e.
AB = 72° < 180°, then the arc is equal to the angle, i.e.
![]() AB =
AB = ![]() AOB, where the angle
AOB, where the angle ![]() AOB is central.
AOB is central.
ΔAOB is isosceles (OA = OB = r), where
![]() OAB =
OAB = ![]() OBA = (180° - 72°) : 2 = 54°.
OBA = (180° - 72°) : 2 = 54°.
Then ΔAOB is equilateral.
The radii of the circle circumscribed about the polygon are the bisectors of its angles, so each angle of the polygon is 54° • 2 = 108°.
Knowing that
αn = ![]() • 180°
• 180°
108° •n = (n - 2) • 180°
108° •n - 180°•n = - 360°
-72° •n = - 360°
n = 5
Answer: n = 5.
***
Formulas for calculating the area of the regular polygon, its side and the radius of the inscribed circle.

Given:
A1A2A3...An is the regular polygon
R is the radius of the circumscribed circle
r is the radius of the inscribed circle
an is the side of the polygon
Prove:
1) the area of the regular polygon is equal to half the product of the perimeter of the polygon by the radius of the inscribed circle
Sn = ![]() Pn • r
Pn • r
2) the side of the regular polygon is equal to twice the product of the radius of the circumscribed circle by the sine of the angle equal to the number from the division of 180° by n - the number of sides of the polygon
an = 2R • Sin (![]() )
)
3) the radius of the inscribed circle is equal to the product of the radius of the circumscribed circle by the cosine of the angle equal to the number from the division of 180° by n - the number of sides of the regular polygon
r = R • Cos (![]() )
)
Proof:
1) By connecting the point O to the vertices of the regular polygon, we obtain triangles Δ A1A2O = Δ A2A3O = ... = Δ A1AnO, where the number of all triangles in the polygon = n.
S (Δ A1A2O) = ![]() • A1A2 • OH1 =
• A1A2 • OH1 = ![]() • an • r.
• an • r.
Then the area of the polygon is equal to the sum of the areas of all triangles
Sn = S (Δ A1A2O) • n = ![]() • an • r • n = (
• an • r • n = (![]() • an • n) • r =
• an • n) • r = ![]() Pn • r
Pn • r
***
2)
Since the angle in the polygon is given by formula
αn = ![]() • 180°, we see that the angle
• 180°, we see that the angle ![]() A1 in the triangle A1H1O is half the angle of the polygon.
A1 in the triangle A1H1O is half the angle of the polygon.
![]() A1 =
A1 = ![]() •(
•(![]() • 180°) =
• 180°) = ![]() • 90° =
• 90° = ![]() = 90° -
= 90° - ![]()
Cos A1 = ![]() =
= ![]()
Then A1H1 = Cos A1 • R = Cos (90° - ![]() ) • R = R • Sin(
) • R = R • Sin(![]() )
)
Knowing that an = A1H1 • 2, we obtain
an = 2R • Sin (![]() )
)
***
Examples:
If n=3, then a3 = 2R • ![]() = R•
= R•![]()
If n=4 (the square), then a4 = 2R • Sin45° = 2R • ![]() = R•
= R•![]()
If n=6 (the regular hexagon), then a6 = 2R • 0,5 = R
***
3)
Sin A1 = ![]()
Then r = R • Sin A1 = R • (90° - ![]() ) = R • Cos (
) = R • Cos (![]() )
)
***
Given:
The regular quadrilateral is the square
| R | r | a4 | P | S | |
| 1 | - | - | 6 | - | - |
| 2 | - | 2 | - | - | - |
| 3 | - | - | - | - | 16 |
what are the radii of the inscribed and circumscribed circumference, the sides, perimeter and area of the regular polygon – the square
R, r, a4, P, S = ?
Solution:
1) If the side of the square a4 = 6 and since given is the square, we see that
the perimeter of the square P = 4 • a4 = 4 • 6 = 24
The area of the square S = a42 = 62 = 36
Since the area of the square can be found by the formula S4 = ![]() P4 • r, we see that the radius of the inscribed circle
P4 • r, we see that the radius of the inscribed circle
r = ![]() =
= ![]() = 3
= 3
Since the number of sides n=4, we see that a4 = R•![]()
The radius of the circumscribed circle R=![]() =
= ![]() =
=![]() =
=![]()
2) If r=2, then the radius of the circumscribed circle
r = R • Cos (![]() ) = R • Cos 45° = R •
) = R • Cos 45° = R • ![]()
R = 2 • ![]() = 2
= 2![]()
Since the number of sides n=4, then the side of the square
a4 = R•![]() = 2
= 2![]() •
• ![]() = 4
= 4
Then the perimeter of the square P = 4 • a4 = 4 • 4 = 16
The area of the square S = a42 = 42 = 16
3) If the area of the square S = 16, then the side of the square
a42 = 16 ![]() a4 = ±
a4 = ±![]() . But a4 = -
. But a4 = -![]() does not satisfy the condition of the problem.
does not satisfy the condition of the problem.
Therefore, a4 = ![]() = 4
= 4
Then the perimeter of the square P = 4 • a4 = 4 • 4 = 16
Since the number of sides n=4, then the radius of the circumscribed circle
a4 = R•![]()
![]() 4 = R•
4 = R•![]()
![]() R =
R = ![]() = 2
= 2![]()
Then the radius of the inscribed circle
r = R • Cos (![]() ) = R • Cos 45° = 2
) = R • Cos 45° = 2![]() •
• ![]() = 2
= 2
***
Given:
Δ ABC is equilateral,
the perimeter of the triangle
PΔ = 18 cm
Find: the side of a square inscribed in the same circle
a4 = ?
Solution:
Since Pn = n • an , we see that the side of the triangle
18 = 3 • a3 ![]() a3 = 6
a3 = 6
Then the radius of the circumscribed circle
a3 = R•![]()
![]() R =
R = ![]() = 2
= 2![]()
Then the side of the square a4 = ![]() • R =
• R = ![]() • 2
• 2![]() = 2
= 2![]()
Answer: 2![]() .
.
***
Given:
ABCD is the square,
the side of the square a4 = 6
Calculate: what is the doubled radius of the inscribed circle 2r = ?
Solution:
Since the area of the square can be found by the formula S4 = ![]() P4 • r, then the radius of the inscribed circle
P4 • r, then the radius of the inscribed circle
r = ![]() =
= ![]() = 3 (cm)
= 3 (cm)
Therefore, 2r = 2 • 3 = 6 (cm).
Answer: 6 cm.
***
Given:
the square, the regular hexagon are inscribed in the circle (O;r) of the center at the point O and the radius r ;
the perimeter of the hexagon P6 = 48 cm
Find: the perimeter of the square P4 = ?
Solution:
Since the formula of the perimeter of the hexagon P6 = 6 • a6 , then the side of the hexagon a6 = 48 : 6 = 8 (cm)
Since given is a regular hexagon for n=6, then
a6 = 2R • 0.5 = R
Since given is one circle, the radii of the circumscribed circle are equal, i.e. R4 = R6 = 8 cm
Then the side of the square a4 = R•![]() = 8
= 8![]() cm
cm
Therefore, the perimeter of the square P4 = 4 • 8![]() = 32
= 32![]() (cm)
(cm)
Answer: P4 = 32![]() cm.
cm.

Given:
ABCDEF is the regular hexagon
BF = 1.5 cm
Find: the area of the hexagon
SABCDEF = ?
Solution:
We draw the diagonal AD and consider the isosceles triangle ΔABF.
By the property of an isosceles triangle AO - is the median.
Therefore, FO = OB = BF : 2 = 1.5 : 2 = 0.75 (cm)
Since the hexagon is regular, we see that using the formula to calculate the angles of the regular polygon
αn = ![]() • 180°, we obtain
• 180°, we obtain
α6 = ![]() • 180° = 120°
• 180° = 120°
Then the angle ![]() BAO = 60°
BAO = 60°
Consider the triangle ΔAOB, where the angle ![]() O = 90°.
O = 90°.
Sin 60° = ![]()
![]()
![]() =
=![]()
![]() AB =
AB = ![]() =
=![]() (cm)
(cm)
Then the perimeter of the hexagon
P6 = 6 • ![]() = 3
= 3![]() (cm)
(cm)
Then the radius of the inscribed circle
r6 = OF = ![]() cm
cm
Therefore, the area of the hexagon
S6 = ![]() • P6 • r6 =
• P6 • r6 = ![]() =
= ![]() (см2)
(см2)
Answer: SABCDEF =![]() cm2.
cm2.
***
Given:
A1A2A3A4A5A6 is a regular hexagon inscribed in a circle(O; R)
B1B2B3B4B5B6 is a regular hexagon, circumscribed about the circle(O; R)
OH = r
OH1 = R

![]() = ?
= ?
Solution:
1)
Consider the hexagon A1A2A3A4A5A6
The sides of the hexagon are equal to the radii of the circumscribed circle A1A2 = A2A3 = A6A1 = R
Knowing that S (A1A2A3A4A5A6) = ![]() P • r =
P • r = ![]() 6Rr = 3R•r
6Rr = 3R•r
Consider the triangle ΔOHA6 is right, since the radius of the inscribed circle is perpendicular to the side of the hexagon r ![]() A1A6
A1A6
Since the point O - is the point of intersection of bisectors, we see that R - is the bisector of the angle ![]() A1A6A5
A1A6A5
Knowing that ![]() OA6A1 = 60°, we obtain
OA6A1 = 60°, we obtain
Sin 60° = ![]()
![]() r = Sin 60° • R =
r = Sin 60° • R = ![]()
Therefore, the area of the hexagon
S (A1A2A3A4A5A6) = 3R •![]() =
=![]() R2
R2
2)
Consider the hexagon B1B2B3B4B5B6
B1B2 = ... = B6B1 = OB5 , where OB5 - is the radius of the circumscribed circle about a given regular polygon, namely the hexagon B1B2B3B4B5B6
S (B1B2B3B4B5B6) = ![]() • (6 • OB5) • R
• (6 • OB5) • R
Consider ΔH1OB5 - is a right triangle, since R - of the inscribed circle in the polygon B1B2B3B4B5B6:
R ![]() B5B6
B5B6
Then ![]() OB5H1= 60°. Therefore
OB5H1= 60°. Therefore
Sin 60° = ![]()
![]() OB5 = 2R
OB5 = 2R![]()
Then the area of the hexagon is B1B2B3B4B5B6
S (B1B2B3B4B5B6) = ![]() • 6 • 2R
• 6 • 2R![]() • R = 2
• R = 2![]() R2
R2
Then the proportion of the areas of the hexagons
![]() = 2
= 2![]() R2 •
R2 • ![]() =
= ![]()
Answer: ![]()
***