Угол между векторами и скалярное произведение векторов

Теоретический урок по предмету математики для решения задач по теме "Векторы".

Содержание данной страницы электронного справочника для школьников:

Свойства векторов

1) Вектор коллинеарный с вектором

2) ↑↑↑↑

3) =

4) = -

5) Дано: система координат

модуль вектора = 5

= 12

Найдите: OA

Решение:

OA== 13

OA = = 13

Ответ: OA = 13

***

 

Пусть и - данные векторы.

1) Отложим от точки O векторы = и =

2) Если ↑↓- противоположно направленные векторы, то лучи OA и OB образуют угол AOB

3) Если ↑↑- сонаправленные векторы, то угол между векторами и равен 0°.

Угол между двумя векторами и обозначается так:

 

Определение:

Два вектора называются перпендикулярными, если угол между ними равен 90°.

***

 

Задача 86.

Дано:

ABCD - квадрат

AC ∩ BD = O

 

Найти: углы между векторами BAC, DAB = ?

Вычисление:

a) Т.к. AC - диагональ квадрата, то она делит угол A пополам. Тогда угол между векторами = 45°

б) Т.к. ABCD - квадрат, то градусная мера угла между векторами = = 90°, т.е. прямой угол.

***

 

Наверх

Скалярное произведение векторов

Задача 87.

Дано:

ABCD - ромб

BD = AB; AC ∩ BD = 0

 

Вычислите: угол, образованный векторами

и , и , и = ?

Решение:

а) По определению ромба ΔABD - равносторонний (AB = AD = BD).

Значит, все углы в треугольнике равны 60°. Тогда угол между векторами = 60°

б) Т.к. векторы ↑↑сонаправленные, то угол между векторами = 0°

в) Т.к. векторы ↑↓ - противоположно направленные, то угол между векторами = 180°

***

 

Определение:

Скалярным произведением двух векторов (формула 1) называется произведение длин этих векторов на косинус угла (Cos) между ними.

Обозначение: или

= *cos (a,b)     (1)

Из формулы скалярного произведения векторов через косинус угла (1) следует:

1) скалярное произведение векторов больше нуля, если угол между векторами меньше 90°, т.е.

>0, если <90°

скалярное произведение векторов меньше нуля, если угол между векторами больше 90°, т.е.

<0, если >90°

2) Если ↑↑ - сонаправленные векторы, то угол между векторами равен нулю градусов, т.е. =0° =

3) Если - перпендикулярные векторы и =90° Cos 90° = 0, то = 0

Верно и обратное, т.е. если = 0

Вывод: = 0

***

 

Задача 88.

Дано:

Векторы

=2

=3

Угол α = 90°

Найти: скалярное произведение векторов

Решение:

Используя формулу скалярного произведения векторов через косинус угла, получаем

= •• Cos 90° = 2 • 3 • 0 = 0

Ответ: = 0

***

 

Скалярный квадрат

***

 

Задача 89.

Дано:

ΔABC - равносторонний

AB = a

 

Найти: скалярное произведение векторов 1) 2)

Решение: В равностороннем треугольнике все углы равны 60°.

1) = •Cos () = • =

2) = •Cos (120°) = -

***

 

Задача 90.

Дано:

Векторы

=2; =3

1) угол α = 45°

2) α = 135°

 

Найти: скалярное произведение векторов

Решение:

1) = •Cos 45° = 2 • 3 • = 3

2) = •Cos 135° = 2 • 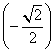3 • = -3

Ответ: 1) 3; 2) -3

***

 

Задача 91.

Дано:

ΔABC - равносторонний

AB = a

BD - высота

 

Найти: скалярное произведение векторов

1)

2) 3)

Решение:

1) = •Cos 120° = • (-Cos 60°) = -

2) т.к. векторы перпендикулярны BDAC = 0

3) = =

Ответ:1) -; 2) 0 ; 3)

 

Задача 92.

Дано:

ABCD - ромб

BD ∩ AC = 0

BD = AB

1) ;

2) ;

 

Найти: величину угла между векторами

1) ; 2)

Решение:

1) Рассмотрим ΔABC - равнобедренный, т.к. AB=BD.

Зная, что в ромбе все стороны равны, получаем ΔABD - равносторонний.

Тогда DAB =BDA = 60°

По свойству ромба следует, что ADC = 120°

Тогда угол между векторами =120°

 

2) Т.к. стороны параллельны и векторы сонаправлены:

BA || CD и ↑↑ , тогда векторы параллельны ||, поэтому векторы равны =.

Рассмотрим треугольник ΔCBD - равнобедренный, т.к. две стороны равны: BD=BC.

По определению ромба ΔCBD - равносторонний.

Значит, угол BDC = 60°

По свойству ромба угол ADC = 120°.

Тогда угол между векторами =120°.

Ответ: 1) =120°; 2) =120°.

***

 

Наверх

Скалярное произведение векторов в координатах

Теорема:

Если два вектора имеют координаты {x₁; y₁}; { x₂; y₂}, то скалярным произведением двух векторов (формула 2) называется произведение их координат:

(2)

 

Доказательство:

1 случай.

Если какой-нибудь вектор - нулевой, то равенство (2) выполняется очевидно.

2 случай.

Если векторы и - неколлинеарны.

Отложим векторы от произвольной точки O.

Рассмотрим треугольник ΔOBA.

Известно, что формула косинуса

c² = a² + b² - 2ab • Cos α, получаем равенство

AB­­² = OB² + OA² - 2 • OB • OA • Cos α (3)

Учитывая значения (*) = ; = ; = ; а также, что OA = ||; OB = || ; AB = ||, подставив значения (*) в равенство (3), получаем

||² = ||² + ||² - 2 (4)

Используя формулу для вычисления длины вектора по его координатам, получаем

=; =.

Т.к. = {x₂ - x₁; y₂ – y₁}, то, используя формулу для вычисления расстояния между двумя точками

, получаем

|| = .

Тогда из равенства (4) следует

(x₂ - x₁)² + (y₂ – y₁)² = x₂² + y₂² + x₁² + y₁² - 2

x₂² -2 x₂ x₁ + x₁² + y₂² – 2 y₂y₁ + y₁² = x₂² + y₂² + x₁² + y₁² - 2

-2 x₂ x₁– 2 y₂y₁ = - 2

= x₂ x₁ + y₂ y₁

***

 

Следствия:

1) Если векторы перпендикулярны, т.е.

{x₁; y₁}{ x₂; y₂} x₁ x₂ + y₁ y₂ = 0

2) По определению скалярного произведения двух векторов (формула 1)

= •• Cos α

Cos α =

Формула для нахождения косинуса угла через координаты векторов: 

Для вычисления синуса и тангенса угла между векторами через косинус угла используются формулы приведения и тригонометрические функции.

 

***

 

Наверх

Скалярное векторное произведение

Задача 93.

Если {; -1}; {2; 3}, то = 0,5 + (-3) = -2,5

***

 

Задача 94.

Если {x; -1}; {3; 2} и векторы перпендикулярны , тогда = 3x - 2 0 = 3x - 2 2 = 3x x =

***

 

Задача 95.

Дано:

Координаты точек

A(2;8), B(-1;5), C(3;1)

 

Найти: косинус угла между векторами Cos A = ?

Решение:

Т.к. каждая координата вектора равна разности соответствующих координат его конца и начала

{b₁ – a₁; b₂ – a₂}, тогда

= {} = {}

= {} = {}

Используя формулу для нахождения углов через координаты векторов

Cos A = , получаем

Cos A = ===

Ответ: Cos A =

***

 

Длина вектора

Задача 96.

Дано:

угол между векторами равен = =60° ,

длины векторов || = 1, || = || = 2

 

Найти: произведение векторов ()= ?

Решение:

()=+= ||•||•Cos 60° + ||•||•Cos 60° = 1 + 2 = 3

Ответ: ()= 3

***

 

Задача 97.

Дано:

=, =

длина векторов ||=||=1

- перпендикулярные векторы

Найти: произведение векторов = ?

Решение:

= ()•() = 3² + 12 - 2- 8² =

= 3² + 10 - 8² = 3||² + 0 - 8||² = -5.

Ответ: = -5.

***

 

Задача 98.

Дано:

{1,5 ; 2}, {4 ; -0,5}

 

Найти: произведение векторов = ?

Решение:

= x₁ x₂ + y₁ y₂ = 6 + (-1) = 5

Ответ: = 5.

***

 

Задача 99.

Дано:

{0 ; -3}, {5 ; x}

- перпендикулярные векторы

 

Найти: произведение векторов = ?

Решение:

= x₁ x₂ + y₁ y₂

0 = 0 + (-3x)

3x = 0

x = 0

Ответ: при x=0, .

***

 

Задача 100.

Дано:

Координаты точек

A(2;8), B(-1;5), C(3;1)

 

Найти: косинус угла векторов

1) Cos B = ?

2) Cos C = ?

Решение:

1)

Т.к. каждая координата вектора равна разности соответствующих координат его конца и начала

{b₁ – a₁; b₂ – a₂}, тогда

= {} = {}

= {} = {}

Используя формулу для нахождения углов через заданные координаты векторов

Cos B = , получаем

Cos B = == 0

2)

= {} = {}

= {} = {}

Cos C = ===

Ответ: Cos B =0, Cos C =

***

 

Задача 101.

Дано:

, где i и j – координатные векторы

 

Найти: длину вектора || = ?

Решение:

Найдем координаты вектора .

{3; -4}

Т.к. длина вектора равна квадратному корню из суммы квадратов его координат || = , тогда получаем

|| = = = 5.

Ответ: || = 5.

***

 

Задача 102.

Дано:

ABCD - ромб

AB =, AD =

 

Доказать: диагонали ромба в точке пересечения перпендикулярны

ACBD или =0

Доказательство:

Т.к. ABCD - ромб - параллелограмм, то векторы параллелограмма ,

= -

= (+) (-) = - ² + ² - = ² -² = =||² -||² = 0. Поэтому угол между векторами = 90°. Значит, диагонали ромба в точке пересечения перпендикулярны ACBD.

***

 

Задача 103.

Дано:

треугольник ΔABC - равнобедренный

AM - медиана

 

Доказать:

1) 4AM² = AB² + AC² + 2AB • AC • Cos A

2) CH = AM

Доказательство:

1) Т.к. точка M - середина BC, тогда

2=

Значит, (2) • (2) = ()() =

= AB² + 2AB + 2AB • AC • Cos A + AC² = AB² + AC² + 2AB • AC • Cos A

Получаем 4AM² = AB² + AC² + 2AB • AC • Cos A

 

2) По формуле, полученной выше, следует

4CH² = AC² + BC² + 2AC • BC • Cos C

Т.к. треугольник ΔABC - равнобедренный, тогда AB = BC, A = C Cos A = Cos C

Получим, что 4CH² = AC² + BC²(=AB²) + 2AC • BC(=AB) • Cos C (= Cos A)

4CH² = AC² + AB² + 2AC • AB • Cos A

4CH² = 4AM²

=

2CH = 2AM | : 2

CH = AM

***

 

Задача 104.

Дано:

ABCD - выпуклый четырехугольник

BD = d₁ и AC = d₂ - диагонали

d₁ ∩ d₂ = O - точка пересечения диагоналей

 

Доказать:

Площадь четырехугольника равна половине произведения диагоналей на синус острого угла между ними

S_ABCD= d₁ • d₂ • Sin α

Доказательство:

Площадь четырехугольника - сумма площадей четырех треугольников.

S_ABCD= S₁ + S₂ + S₃ + S₄ , где

S₁ = S_ΔAOB ; S₂ = S_ΔCOB ; S₃ = S_ΔCOD ; S₄ = S_ΔAOD

S₁ = BO • OA • Sin α

S₂ = BO • OC • Sin (180° - α) = BO • OC • Sin α

S₃ = CO • OD • Sin α

S₄ = AO • OD • Sin (180° - α) = AO • OD • Sin α

Сложив S₁ + S₂ + S₃ + S₄, получаем

S_ABCD= BO • Sin α (OA+OC) +

+ OD • Sin α (CO+OA)

Т.к. OA+OC = AC, CO+OA = AC, BO + OD = BD тогда

S_ABCD=BO • AC • Sin α +OD • AC • Sin α =BD • AC • Sin α

 

Формула площади выпуклого четырехугольника:

S_ABCD= d₁ • d₂ • Sin α

 

 

***

 

Задача 105.

Дано:

два вектора образуют угол α = 150°,

длины векторов || = 2 , || = 2

 

Найти: длину вектора |2-| = ?

Решение:

BC² = AB² + AC² - 2 AB • AC • Cos 150°

BC² = 48 + 4 - 2 • 4• 2 • (-) = 52 + 24 = 76

BC = = 2

Ответ: BC = |2-| = 2

***

 

Задача 106.

Дано:

Треугольник ΔABC

Угол B = 45°, C = 70°

a=24,6

 

Найти: Угол в градусах A, стороны b, c

Решение:

A = 180° - (45° + 70°) = 75°

 

Используя теорему синусов

, получаем выражение

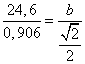
b = ≈ 19,2

c = ≈

≈ 25,5

Ответ: A = 75°; b ≈ 19,2; c ≈ 25,5.

***

 

Задача 107.

Дано:

длины векторов || = 5, || = 8,

угол между 2 векторами =60°

 

Найти: значение векторов

1) ||= ?

2) ||= ?

Решение: По теореме косинусов

1)

AC² = AB² + BC² - 2AB • BC • Cos 120°

AC² = 25 + 64 - 80 • (- 0,5) = 129

AC = ±, но AC = - не удовлетворяет решению задачи. Значит, AC =.

 

2) BC² = AB² + AC² - 2AB • AC • Cos 60°

BC² = 89 - 80 • 0,5 = 49

BC = ±, но BC = - 7 не удовлетворяет решению задачи. Значит, BC = 7.

Ответ: || =; || = 7.

***