Тригонометрия

Корзина

Пусто

60р.

ΔABC - прямоугольный треугольник
Катеты a = BC, b = AC
Гипотенуза c = AB

Как пользоваться онлайн-калькулятором. В форме укажите известные параметры прямоугольного треугольника:
а) 2 катета,
б) катет и гипотенуза,
в) катет и противолежащий острый угол,
г) гипотенуза и острый угол.
Заполните поле "Текст с картинки". Нажмите "Решить".

Калькулятор сторон и углов треугольника

Найти синус, косинус, тангенс, секанас, косеканс угла онлайн

Содержание электронного справочника по математике для школьников на данной онлайн странице:

– задачи 54 - 56 представлены с примерами решений и ответами по теме "Тригонометрические функции";
– в тестах с номерами 57 - 63 рабочей тетради рассматривается, как решать задания по предмету "Тригонометрия за 9 класс", если требуется определить синус, косинус, тангенс, используя основные формулы приведения;
– задачи, как вычислять координаты точки через косинус и синус угла, объясняются в контрольных работах по тригонометрии 64 - 68;
– тема "Формула площади треугольника, параллелограмма" представлена в самостоятельных работах 69 - 71 учебника;
– теорема синусов рассматривается в гдз по геометрии с номерами 72 - 74;
– теорема косинусов для треугольника рассматривается в примере 75 данной тетради-задачника.

Основные тригонометрические функции

Рассмотрим прямоугольный треугольник ΔOMD.

;

Но OM=r=1, MD=y, OD=x

Тогда

Sin α = y 0 ≤ y ≤ 1; 0 ≤ Sin α ≤ 1

Cos α=

Cos α = x –1 ≤ x ≤ 1; –1 ≤ Cos α ≤ 1

Определение:

Для любых углов α (читается: альфа): 0°≤ α≤180°

Sin α (синусом угла α) называется ордината точки M, а

Cos α (косинусом угла α) называется абсцисса точки M.

Задача 54.

Дано:

Окружность (0;r)

Координаты точек A(1;0),

B(–1;0), M₁(0;1); M₂(;)

Найти:

1) принадлежат ли данные точки окружности,

2) синус, косинус, тангенс углов

Решение:

1) Проверяем точку A

x² + y² = r²

1² + 0² = 1²

1=1 (верно, данная точка принадлежит окружности)

Проверяем точку B

(–1)² + 0² = 1²

1² = 1²

1=1 (верно)

Проверяем точку M₁

0² + 1² = 1²

1=1 (верно)

Проверяем точку M₂

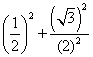=(1)²

= 1

1=1 (верно)

2) SinAOM₁=1, CosAOM₁=0

tgAOM₁≠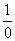(не определяется)

SinAOM₂= , CosAOM₂= ,

tgAOM₂= = =

SinAOB=0, CosAOB=–1

tgAOM=== 0

0	90	180
синус Sin 0° = 0	синус Sin 90° = 1	синус Sin 180° = 0
косинус Cos 0° = 1	косинус Cos 90° = 0	косинус Cos 180° = –1
тангенс tg 0° = = 0	тангенс tg 90° ≠ (не определяется)	тангенс tg 180° = 0

tg α =

Основное тригонометрическое тождество (0°≤ α ≤180°)

Дуга ACB является частью окружности, заданное уравнением

x² + y² = 1, где

x = Cos α; y = Sin α

Тогда Cos²α + Sin²α = 1

***

Задача 55.

Дано:

Косинус угла Cos α =

Вычислите: синус угла альфа Sin α = ?

Решение:

Cos²α + Sin²α = 1

Sin²α = 1 – Cos²α

Sin α =

Учитывая условия, что 0°≤ α≤180°, 0 ≤ Sin α ≤ 1, получаем

Sin α = ==

Ответ: Sin α =

***

Задача 56.

Дано:

Синус угла Sin α =

Найти: косинус угла альфа Cos α = ?

Решение:

Cos²α + Sin²α = 1

Cos²α = 1 – Sin²α

Cosα =

Cosα =	Cosα = –
Cosα =	Cosα = –

Ответ: Cosα =

***

Наверх

Формулы приведения

Таблица. Тригонометрические формулы приведения - синус, косинус в тригонометрии

Sin (90° – α) = Cos α	Cos (90° – α) = Sin α (0°≤ α≤90°)
Sin (180° – α) = Sin α	Cos (180° – α) = – Cos α (0°≤ α≤180°)

Задача 57.

Дано:

Косинус угла Cos α =

Найти: синус угла альфа Sin α = ?

Решение:

Cos²α + Sin²α = 1

Sin²α = 1 – Cos²α

Sin α =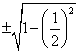

Учитывая условие, что 0 ≤ Sin α ≤ 1, получаем

Sin α = ==

Ответ: Sin α =

***

Задача 58.

Дано:

Косинус угла Cos α =

Найти: синус угла альфа Sin α = ?

Решение:

Cos²α + Sin²α = 1

Sinα =

Sin α = ==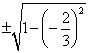

Учитывая условие, что 0 ≤ Sin α ≤ 1, получаем

Sin α ==

Ответ: Sin α =

***

Задача 59.

Дано:

Синус угла Sin α =

Найти: косинус угла альфа Cos α = ?

Решение:

Cos²α + Sin²α = 1

Cos²α = 1 – Sin²α

Учитывая условие, что –1 ≤ Cos α ≤ 1, получаем

Cosα = =

Cosα =

Ответ: Cosα =

***

Задача 60.

Дано:

Синус угла Sin α =0

Найти: косинус угла альфа Cos α = ?

Решение:

Cos²α + Sin²α = 1

Cos²α = 1 – Sin²α

Учитывая условие, что –1 ≤ Cos α ≤ 1, получаем

Cosα = =±1

Ответ: Cosα =±1

***

Задача 61.

Дано:

Косинус угла Cos α = 1

Найти: тангенс угла альфа tg α = ?

Решение:

tg α =

Cos²α + Sin²α = 1

Sinα = ±

Учитывая условие, что 0 ≤ Sin α ≤ 1, получаем

Sinα = 0

Используя формулу для тангенса, получаем

tg α = tg α = 0

Ответ: tg α = 0

***

Задача 62.

Дано:

Косинус угла Cos α =

Найти: тангенс угла альфа tg α = ?

Решение:

tg α =

Cos²α + Sin²α = 1

Sinα = ±=±

Учитывая условие, что 0 ≤ Sin α ≤ 1, получаем

Sinα =

tg α == ==

Ответ: tg α =

***

Задача 63.

Дано:

Углы 120°, 135°, 150°

Найти: синус, косинус, тангенс углов

Sin α =? Cos α = ? tg α = ?

Решение:

Sin 120° = Sin (180° - 60°) = Sin 60° =

Cos 120° = Cos (180° - 60°) = - Cos 60° = -

tg 120° = = • (-2) = -

Sin 135° = Sin (180° - 45°) = Sin 45° =

Cos 135° = Cos (180° - 45°) = - Cos 45° = -

tg 135° = = • = -1

Sin 150° = Sin (180° - 30°) = Sin 30° =

Cos 150° = Cos (180° - 30°) = - Cos 30° = -

tg 150° = = • = -1 • = -

***

Наверх

Координаты точки через косинус и синус угла

Задача 64.

Дано: график окружности

Точка A(x;y), y>0

A(x;y) не лежит на окружности (0;r)

Угол α

Доказать:

x= OA • Cos α

y= OA • Sin α

Доказательство:

Точка M лежит на окружности с центром в начале координат и на прямой OA, т.е.

M=окр(0;r=1) ∩ OA или окр(0;r=1) ∩ OA=M

Координаты точки M(x=Cos α; y=Sin α)

Координаты вектора {Cos α; Sin α}, т.к. OM - радиус-вектор точки M.

С помощью формулы для вычисления длины вектора по его координатам получаем

====1

Тогда =OA•

{OA•Cos α; OA• Sinα} (*)

Т.к. - радиус-вектор точки A, тогда

{x;y} (**)

Тогда, учитывая условия (*) и (**), получаем

формула, как найти координаты точки через косинус и синус угла:

x= OA • Cos α;

y= OA • Sin α

***

Задача 65.

Дано:

OA=3

α= 45°

Найти: координаты точки A(x;y)

Решение:

Используя формулы для вычисления координаты точки через косинус и синус угла, получаем

x= OA • Cos α = 3 • Cos 45°= 3 • =

y= OA • Sin α = 3 • Sin 45°=

Ответ: A(;)

***

Задача 66.

Дано:

координаты точки A(2;2)

окружность с центром в начале координат (0;0)

Найти: угол α

Решение:

Т.к. по условию координаты точки A(2;2).

Используя формулы для вычисления координаты точки через косинус и синус угла, получаем

A (OA • Cos α; OA • Sin α);

Тогда OA • Cos α = 2

Используя формулу для вычисления расстояния между двумя точками , получаем

OA = =

• Cos α = 2

Cos α = = α =45°

Ответ: α =45°

***

Задача 67.

Дано: длина отрезка и величина угла

1) OA=1,5

α= 90°

2) OA=5

α= 150°

3) OA=2

α= 30°

Найти: координаты точки A(x;y)

Решение:

1) x= OA • Cos α = 1,5 • Cos 90°= 1,5 • 0 = 0

y= OA • Sin α = 1,5 • Sin 90°= 1,5 • 1 = 1,5

2) x= OA • Cos α = 5 • Cos (180° - 30°)= 5 • (- Cos 30°) = -

y= OA • Sin α = 5 • Sin (180 - 30°) = 5 • Sin 30° = 5 • == 2,5

3) x= OA • Cos α = 2 • Cos 30° = 2 • =

y= OA • Sin α = 2 • Sin 30° = 2 • = 1

Ответ: 1) (0; 1,5) 2) (-; 2,5) 3) (;1)

***

Задача 68.

Дано:

1) A(0;3)

2) B(–;1)

Найти: угол α

Решение:

1) Т.к. по условию координаты точки A(0;3).

Используя формулы для вычисления координаты точки через косинус и синус угла, получаем

A (x=OA • Cos α; y=OA • Sin α);

Тогда x=OA • Cos α = 0

y= OA • Sin α = 3

Используя формулу для вычисления расстояния между двумя точками , получаем

OA = = 3

3 • Cos α = 0

Cos α = 0

α = 90°

2) Т.к. по условию координаты точки B(-;1).

Используя формулы для вычисления координаты точки через косинус и синус угла, получаем

B (x=OB • Cos α; y=OB • Sin α);

Тогда x = OB • Cos α = - (*)

Используя формулу для вычисления расстояния между двумя точками , получаем

OB = == 2

Используя условие (*), получаем

2 • Cos α = -

Cos α = -

α = 150°

Ответ: 1) 90° ; 2) 150°

***

Теорема:

Площадь треугольника равна половине произведения двух его сторон на синус (Sin) угла между ними.

Дано:

Треугольник ΔABC

Стороны треугольника

BC=a, AC=b, AB=c

S - площадь треугольника

Доказать:

S_Δ_ABC=a • b • Sin C

Доказательство:

Площадь треугольника равна половине произведения основания треугольника на его высоту. Поэтому

S_Δ_ABC=a • h (*), где h – высота треугольника, a - основание

Но высота h = b • Sin C (**).

Используя условие (**) в формуле (*), тогда

Формула площади треугольника через синус, основание и высоту

S_ΔABC=• a • b • Sin C

a = ; b =

***

Задача 69.

Дано:

1) AB = 6

см

AC = 4 см

A = 60°

2) BC = 3 см

AB = 18см

B = 45°

3) AC = 14 см

CB = 7 см

C = 48°

Найти: площадь треугольника S_Δ

Решение:

Используя формулу площади треугольника через синус, основание и высоту, получаем

S_Δ=• a • b • Sin α; Sin 60° =

1) S_Δ=• 6• 4 • = 6• = 6= 12см²

2) S_Δ=• 3 • 18• === 27 см²

3) S_Δ=• 14 • 7 • Sin 48°, где Sin 48° ≈ 0,7

Тогда S_Δ= 7 • 7 • 0,7 ≈ 34,3 см²

Ответ: 1) 12см² 2) 27 см² 3) 34,3 см²

***

Задача 70.

Дано:

Площадь треугольника S_Δ_ABC= 60 см²

Сторона AC = 15

Угол A = 30°

Найти: сторону AB

Решение:

S_Δ= • AC • AB • Sin 30° = • AC • AB • = • AC • AB;

AB = = = 16 см

Ответ: AB = 16 см

***

Задача 71.

Теорема:

Площадь параллелограмма равна произведению двух его смежных сторон на синус (Sin) угла между ними.

Дано:

ABCD - параллелограмм

AB = a

AD = b

S - площадь параллелограмма

Доказать: S = a • b • SinA = a • b • Sin α

Доказательство:

S = AD • BH

Рассмотрим треугольники ΔABD и ΔBDC. Данные треугольники равны по третьему признаку.

Тогда площади треугольников также равны S_Δ_ABD = S_Δ_BDC

S_Δ_BDC=• BC • CD • Sin α

Тогда площадь параллелограмма

S_ABCD= S_Δ_ABD + S_Δ_BDC= 2 • S_Δ_BDC

S_ABCD=2 • • a • b • Sin α = a • b • Sin α

***

Наверх

Теорема синусов

Теорема синусов для треугольника. Каждая сторона произвольного треугольника пропорциональна синусу противолежащего угла.

Дано:

Треугольник ΔABC

AB=c, BC=a, AC=b

Доказать:

Доказательство:

По теореме о площади треугольника получаем

S_ΔABC=c • b • Sin A (1)

S_ΔABC=a • b • Sin C (2)

S_ΔABC=c • a • Sin B (3)

Из равенства (1) и (2) следует, что

c • b • Sin A = a • b • Sin C

c • Sin A = a • Sin C

Тогда получаем (*)

Из равенства (2) и (3) следует, что

a • b • Sin C =c • a • Sin B

b • Sin C = c • Sin B

Тогда получаем (**)

Из равенств (*) и (**) получаем

- формула синуса треугольника

***

Задача 72.

Дано:

Треугольник ΔABC

Сторона AC = 12 см

Угол A = 75°

Угол С = 60°

Как найти: сторону AB треугольника, площадь треугольника S_Δ_ABC= ?

Решение: Используя теорему синусов, получаем

(*)

B = 180° ─ (60° + 75°) = 45°

Подставив известные значения переменных в равенство (*), получаем

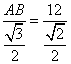
AB = = 6≈ 15 (см)

Т.к. площадь треугольника равна половине произведения двух его сторон на синус (Sin) угла между ними, получаем равенство

S_Δ_ABC=• AB • AC • Sin A = • 15 • 12 • Sin 75° = 90 • 0,9659 ≈ 87 (см²)

Ответ: AB ≈ 15 см, S_Δ_ABC ≈ 87 см².

***

Задача 73.

Дано:

Треугольник ΔABC

Сторона BC = см

Угол A = 45°

Угол С = 30°

Найти: сторону AB треугольника

Решение:

Используя теорему синусов, получаем

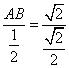
AB = 1 см.

Ответ: AB = 1 см.

***

Задача 74.

Дано:

ABCD – прямоугольник

Диагональ AC = 10 см

Угол BOC = 30°

Найти: Площадь прямоугольника

S_ABCD=?

Решение:

Т.к. ABCD - прямоугольник, тогда по определению прямоугольника ABCD является параллелограммом. Следовательно, он обладает свойствами и признаками параллелограмма.

AC=BD и BD=OD, AO=OC

По признаку параллелограмма BO=OC; OD=AO.

Рассмотрим равнобедренный треугольник ΔBOC (BO=OC).

Т.к. угол BOC = 30°, тогда

OBC = BCO = (180° - 30°) : 2 = 75°, т.к. треугольник Δ BOC - равнобедренный.

Рассмотрим треугольник ΔBCD, где C = 90°.

Угол BDC = 180° - (75° + 90°) = 15°.

По теореме синусов составим соотношения:

CD = 0,9659 • 10 = 9,6 (см)

По теореме Пифагора

BC = = = = 2,8 (см)

Тогда S_ABCD= BC • CD = 2,8 • 9,6 = 25 (см²).

Ответ: S_ABCD= 25 см².

***

Наверх

Теорема косинусов

Теорема косинусов для треугольника. Квадрат любой стороны треугольника равен сумме квадратов других сторон и минус удвоенное произведение этих сторон на косинус (Cos) угла между ними.

Дано:

Треугольник ΔABC