On this webpage you can find the solved tests for geometry of the 8th and 9th grades:
Given:
ABCD is a quadrilateral
M, N, K, E are the midpoints of the sides AB, BC, DC, AD
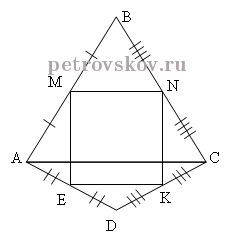
Prove:
The quadrilateral MNKE is a parallelogram
Proof:
Join a point A to a point C. We obtain the triangle ∆ ABC, where MN is the midline of the triangle ∆ ABC, and the triangle ∆ ADC, where EK is the middle line of the triangle ∆ ADC.
By the property of the midline of a triangle ∆ it follows that
MN || AC are parallel and MN=
AC,
EK || AC are parallel and EK= AC.
Then MN || EK are parallel and MN=EK, therefore 
MNKE is the parallelogram (by the first theorem of a parallelogram).
Given:
∆ ABC is a triangle
The length of the triangle side AB = 8.5 cm
The length of the triangle side AC = 5 cm
The height AH = 4 cm, i.e. the segment AH is perpendicular to the side BC
H
BC, i.e. the point H lies on the side BC
Solve:
The area of the triangle = Area ∆ABC = ?
Solution:
Area ∆ABC = BC ∙ AH
By the Pythagorean theorem
BH = 
= 
= 
= 7.5 cm
By the Pythagorean theorem
CH = 
= 
= 3 cm
BC = BH + CH = 3 +7.5 = 10.5 cm
Area ∆ABC = ∙ 10.5 ∙ 4 = 21 cm2
Answer: Area ∆ABC = 21 cm2
***
Given:
ABCD is an isosceles trapezoid
Prove: NE 
KM = 
Proof:
Draw perpendiculars BH and CH1, i.e. BHAD are perpendicular; also CH1AD are perpendicular.
But BH and CH1 cross NE then BRNE and CR1NE are perpendicular.
The sides BH = CH1 and BH || CH1 are parallel.
Therefore BH = KM = CH1 BH 
KM CH1 are parallel as segments between parallel lines.
Therefore the angles are equal 
KON = NR1C = 90º as corresponding angles.
Then KON = EOM = 90º, as vertical angles.
***
Given:
AB is a segment
AC = CB
O is an arbitrary point
Prove:
The OC vector is half of the sum of the other two vectors OA and OB going out of the same point O
(1)
+
(2)
Adding equalities (1) and (2), we get
***
Given:
a, b, c are vectors
Three vectors 
and 
are non-collinear vectors.
The sums and differences of vectors.
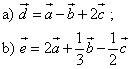
Construction:
By the rule of a polygon
a) 
b) 
=
Prove that the segments connecting the midpoints of the opposite sides of an isosceles trapezoid are perpendicular.
Given:
The quadrilateral ABCD is an isosceles trapezoid
Prove: EF NM = , i.e. the angle of intersection of two segments in an isosceles trapezoid is 90º.
Proof:
Draw parallel lines
MK || AB
MR || CD
We get an isosceles triangle ∆MKR
AB=MK, since the trapezoid is isosceles,
CD=MR, since the trapezoid is isosceles.
Therefore, EF is the midline of the triangle ∆MKR, hence
MH=HR and OK=MO.
BM=MC=AK=RD, since ABMK and MCDR are parallelograms.
Therefore HR=KO.
Then MN is the median, the bisector and the height of the isosceles triangle ∆MKR.
Since MN is the height, we see that the segments MN AD are perpendicular.
By the property of the midline of a triangle ∆ it follows that
EF || KR.
Then EF NM =
***
Prove that the center of a circle inscribed in an isosceles triangle lies on the median drawn to the base.
Given:
an inscribed circle in an isosceles triangle
∆ABC is an isosceles triangle
BH2 is a median
Prove: O BH2, i.e. the center of the inscribed circle lies on the median of an isosceles triangle
Proof:
Draw perpendiculars OH1 ; OH2 ; OH3 to the sides of BC, AC, AB.
Here, from the two points, the same perpendicular to the AC side is drawn, but in the triangle, only one perpendicular can be drawn to the side and only from one point.
Therefore that O BH2
***
Prove that the center of the circle circumscribed around an isosceles triangle lies on the median drawn to the base or to its continuation.
The circumcircle around an isosceles triangle
∆ ABC is an inscribed isosceles triangle
BH3 is a median
Prove: O BH3
Proof:
Draw perpendiculars from the center of the circle
OH1 ; OH2 ; OH3 to the sides of BC, AC, AB.
Here, a perpendicular to the AC side is drawn from two points, but only one perpendicular can be drawn to the side and only from one point in the triangle.
Therefore, O BH3
***
The lemma is a theorem that is subsidiary for the proof of the following theorem.
The lemma about collinear vectors:
If the vectors 
and 
are collinear (where 
), then we can find a such number k that the equality is true 
(the vector is equal to the product of the number k by the vector )
Given: vector a, vector b
The vectors and are collinear, i.e. the vector b is collinear with the vector a.
Prove: there is a such number k that the following equality is true
Proof:
, where k>0, since . Then and 
are the co-directional vectors. 
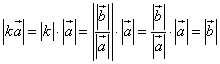
Therefore
***
Case 2.
Let a, b vectors be opposite vectors, i.e. 
Let us take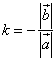 
, where k<0
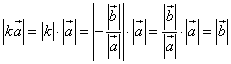
Consequently, 
***
Given:
vector m, vector n
1) 
are oppositely directed vectors,
= 0.5 cm, 
= 2 cm
2) are co-directional vectors,
= 12 cm, = 240 cm
Solve: k – ?
Solution: 1) Since , we see that k<0. Hence
= –
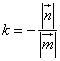= – 4
Answer: k = – 4.
Solution: 2) Since , we see that k>0. Therefore 
= 
= 20.
Answer: k = 20.
***
ABCD is a parallelogram
BD AC = O
M is the midpoint of the segment AO
1) 
2) 
Solve: k – ?
Solution:
1) Since 
, we see that k>0. 
By the property of a parallelogram
, we see that 
Answer: k=
2) Since 
, we see that k<0. , are collinear, since they lie on one straight line. Find the midpoint of OC and call it as the point N.
We see that AM=MO=ON=NC
Since k<0, we see that 
Answer: k= 
***
Given:
1) are oppositely directed vectors,
= 400 mm, = 4dm = 400mm
2) are co-directional vectors, = 
, = 
Solve: k – ?
Solution: 1) Since , we see that k<0. Hence
= –
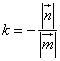= –1
Answer: k = –1.
Solution: 2) Since , we see that k>0. Therefore = 
= 
=5.
Answer: k = 5.
***
Solve the equation: find the values of x, y.
Solution: 1)
y=3
Answer: x=0, y=3
***
Solve the equation: find the values of x, y.
Solution: 2)
–3y = –1 , x= –1
y =
Answer: x= – 1, y=
***
Definition: If 
, where and are the given vectors, x and y are some numbers, then we say that the vector 
is decomposed into vectors and , where x and y are the resolution coefficients.
through vectors 
and 
through and 
through 
and 
through and
Solution:
a) By the parallelogram rule 
(x= 1, y= 1)
b) , 
(x=y= 2)
c) =
+ , = 2 – (x= 2, y = –1)
d) Since = 2 – = 2 +
= – 2(x= 1, y = –2)
***
Given: ABCD is a parallelogram
; 
M
; AM : MC = 4 : 1
Find: 
Solution:
By the parallelogram rule
or 
But 
, then 
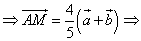
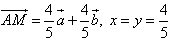
Answer: 
***
Given: vectors and are non-collinear.
a) 
b) 
Solve: the resolution coefficients of the x, y – ?
Solution:
a) 
3 – y = 0, x+1=0 y= 3, x= – 1
b) 
4 – x = 0, 5+y=0 x = 4, y= –5
Answer: a) x= –1, y= 3 б) x = 4, y= –5
***
Given: a figure ABCD is a trapezoid
EF is a middle line of the trapezoid
Prove: EFAD, i.e. the midline of the trapezoid is parallel to its base, 
i.e. the length of the midline of the trapezoid is a half of the sum of the lengths of the trapezoid bases.
Proof:
By the rule of a polygon
+
Adding both expressions, we get
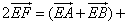
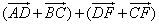
Since E and F are the midpoints of the sides AB and CD, we see that
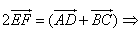
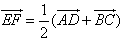
Since 
, we see that 
, and 
Therefore EF || AD and
Theorem: Any vector 
can be decomposed into two non-collinear vectors, and the coefficients of the resolution are determined uniquely.
Given:
vector a, vector b
and are non-collinear vectors.
Prove: 
Proof:
Through the point A and the point B we draw lines parallel to the straight lines containing the vectors and . Find the point C.
Then by the rule of the triangle
Let us remark that the vectors and are collinear, and the vectors are are collinear too.
By the lemma about collinear vectors
, 
Then 
Uniqueness of resolution
Proof:
We know that (1)
Let there be 
(2)
As a result of the difference between expressions (1) and (2) we get
This equality is possible
; 
I.e. 
;
***
Definition: An unit vector is a vector of length is equal to 1.
i and j are coordinate vectors
Since 
and 
are non-collinear vectors, we see that any vector can be decomposed into the vectors and .
I.e. 
, where x and y are the vector coordinates.
{1:2}
{2:–3}
{0;0}
If 
and 
,
then 
if 
and 
***
Find the coordinates of the vectors.
Solution:
{2;3}
{–2;3}
{2;0}
{–3;–4}
{2;–2}
{–4;–5}
***
Find the coordinates of the vectors.
Solution:
{2;3}
{–;–2}
{8;0}
{1;–1}
{0;–2}
{–1;0}
***
Find the sum of the vector from its coordinates.
Solution:
{–3;
} 
{–2;–3} 
{–1;0} 
{0;3} 
{0;1} 
***
The rules that allow you to find the coordinates of the sum, the difference of vectors and the product of a vector by a number from the coordinates of the vectors.
1. A vector with coordinates (a1+ b1;a2 +b2) is called the sum of vectors and with coordinates (a1;a2) and (b1;b2).
Given:
{a1;a2}; {b1;b2}; 
Prove: { a1+ b1;a2 +b2}
is the sum of the coordinates of the vector, i.e. this is the formula how to find the coordinates of a vector through the addition.
Proof:
{ a1+ b1;a2 +b2}
***
Example 1 is about the addition of vectors, how to find the coordinates of vectors:
If the coordinates of the vectors are given {3;2}; {2;5}, then
2. The difference of the vectors and with coordinates {a1; a2} and {b1; b2} is a vector with coordinates {a1 – b1; a2 – b2}.
3. The product of a vector with coordinates {a1; a2} by an arbitrary number k is a vector with coordinates {ka1; ka2}.
Given:
{a1;a2}
k is an arbitrary number
Prove: {ka1; ka2}
is the product of a vector by a number
Proof:
Therefore, the vector {ka1; ka2}
Example 2 is about how to find the vector coordinates:
Find the coordinates of the vector 
if
{1;2}; {0;3}; {–2;3}
Solution:
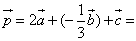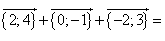{0;6}
{0;6}
Answer: {0;6}
***
Find the coordinates of a vector 
if given are the vectors with coordinates
{–7;–1}; {–1;7}; {4;–6}
Solution:
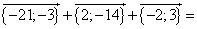
= {–21;–14}
Answer: {–21;–14}
***
Given:
1) 
2) 
Solve: resolution coefficients of x, y – ?
Solution:
1)
By the theorem about the resolution of a vector into two non-collinear vectors:
x=–3, y=7
2)
By the theorem about the resolution of a vector into two non-collinear vectors:
x= –4, y=0
***
Given: the coordinates of the vectors
1) {3;6}; {4;–3}
2) {–5;–6}; {2;–4}
Solve: the difference of vectors –
Solution:
1) –= 
= {–1;9}
–{–1;9}
2) –= 
={–7;–2}
–{–7;–2}
***
Given: the coordinates of the vectors
{–2;–3}; {2;–3}; {0;5}
Solve: the coordinates of the vectors are opposite to the given coordinates.
Solution:
{–2;–3} {2;3}
{2;–3} {–2;3}
{0;5} {0;–5}
***