На данной онлайн странице электронного справочника по математике для школьников представлены следующие готовые домашние задания, решения тестовых заданий по геометрии 9 класса:
Автобус едет из города Анск в город Бинск. На карте город Анск обозначим латинской буквой A, город Бинск – буквой B латинского алфавита.
Соединив точки A и B, получаем отрезок AB. При этом точка A – начало отрезка или пункт отправления автобуса, т.е. откуда едет автобус, точка B – конец отрезка или пункт назначения автобуса, куда движется автобус.
Отрезок AB изображает схему маршрута автобуса.
Направление движения автобуса, или направление маршрута, или направление отрезка AB обозначим стрелкой –>.
Выражение «A –> B» обозначает схематичное движение автобуса из пункта A в пункт B.
Отрезок со стрелкой – направленный отрезок.
Определение:
Вектор – направленный отрезок.
В математике принято обозначать вектор как 
, две латинские буквы со одной стрелкой сверху (произносится: вектор а-б.).
указывает на направление движения: A – начальная точка отрезка, B – конечная точка отрезка.
Часто вектор могут обозначать маленькой буквой 
(произносится: вектор а).
Когда A – начальная точка отрезка и B – конечная точка отрезка совпадают, то есть когда отрезок отсутствует, тогда вектор считается нулевым и обозначается как
, ноль со одной стрелкой сверху. Любая точка на карте, в тетради, на плоскости чертежной доски – нулевой вектор.
Длина отрезка AB, расстояние между городом Анск и Бинск, – абсолютная величина вектора , или модуль вектора
, или длина вектора .
Модуль вектора обозначается как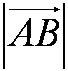 
.
Например, дано = 1,7 км,
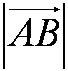= 6 км. В этом случае говорят, что длина вектора а равна 1,7 км (одна целая семь десятых километра), длина вектора AB равна шести километрам.
Длина нулевого вектора обозначается как
и равна нулю:
= 0.
Величина может быть скалярной или векторной.
Величина является скалярной, если содержит численное значение, но не указывает на направление. Например, 5 книг, 10 метров ткани, где цифры «5», «10» – скалярные величины.
Векторная величина или вектор – величина, которая содержит количественное значение и указывает на направление.
Например, автобус едет или совершает перемещение из пункт A в пункт B со скоростью 30 км/ч.
Цифра «30» – скорость автобуса в км/ч – пример векторной величины, так как дано численное значение и указывается направление движения.
Перемещение точки, которая движется в данный момент времени, – вектор с начальной точкой в точке старта движения и с конечной точкой в точке, где данная точка находится в это время.
Длина маршрута движения автобуса из пункта A в пункт E составляет
L = AB + BC + CD + DE = 15 км.
Длина маршрута – скалярная величина, так как дано только количество километров – «15» без указания на направление движения.
Перемещение – вектор
, который соединяет A – точку начала движения автобуса, E – точку остановки движения.
AE = 4 км. Перемещение – векторная величина, где число «4» – количество километров, АЕ – указывает на направление движения, из пункта Анск в пункт Eнск.
Допустим, автобус проехал 30 км: в одну сторону, из Анска в Енск – 15 км, а также обратно, из Енска в Анск – 15 км. В этом примере перемещение равно 0 км и является нулевым вектором.
Лемма – теорема, вспомогательная для доказательства следующей теоремы.
Лемма о коллинеарных векторах:
Если векторы 
и 
коллинеарны (где 
), то можно найти такое число k, что верно равенство 
(вектор равен произведению числа k на вектор )
Дано: вектор a, вектор b
Векторы и – коллинеарные, т.е. вектор b коллинеарен вектору a
Доказать: есть такое число k, что верно равенство
Доказательство:
.
, где k>0,т.к. . Тогда и 
сонаправленные векторы.
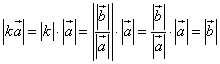
Значит,
***
2 случай.
Пусть a, b - противоположные векторы, т.е. 
Возьмем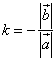 
, где k<0
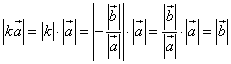
Следовательно, 
***
Дано:
вектор m, вектор n
1) 
– противоположно направленные векторы ,
= 0,5 см, 
= 2 см
2) – сонаправленные векторы ,
= 12 см, = 240 см
Найти: k – ?
Решение: 1) Т.к. , то k<0. Тогда
= –
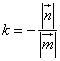= – 4
Ответ: k = – 4.
Решение: 2) Т.к. , то k>0. Тогда 
= 
= 20.
Ответ: k = 20.
***
ABCD – параллелограмм
BD
AC = O
M – середина отрезка AO
1) 
2) 
Найти: k – ?
Решение:
1) Т.к. 
, то k>0. 
По свойству параллелограмма
, тогда 
Ответ: k=
2) Т.к. 
, то k<0. , – коллинеарные, т.к. лежат на одной прямой. Найдем середину OC и обозначим ее точкой N.
Тогда AM=MO=ON=NC
Т.к. k<0, то 
Ответ: k= 
***
Дано:
1) – противоположно направленные векторы,
= 400 мм, = 4дм = 400мм
2) – сонаправленные векторы , = 
, = 
Найти: k – ?
Решение: 1) Т.к. , то k<0. Тогда
= –
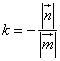= –1
Ответ: k = –1.
Решение: 2) Т.к. , то k>0. Тогда = 
= 
=5.
Ответ: k = 5.
***
Решить уравнение: найти значения x, y.
Решение: 1)
y=3
Ответ: x=0, y=3
***
Решить уравнение: найти значения x, y.
Решение: 2)
–3y = –1 , x= –1
y =
Ответ: x= – 1, y=
***
Определение: Если 
, где и – данные векторы, x и y – некоторые числа, то говорят, что вектор 
разложен на векторы и , причем x и y – коэффициенты разложения
через векторы 
и 
через и 
через 
и 
через и
Решение:
а) По правилу параллелограмма 
(x= 1, y= 1)
б) , 
(x=y= 2)
в) =
+ , = 2 – (x= 2, y = –1)
г) Т.к. = 2 – = 2 +
= – 2(x= 1, y = –2)
***
Дано: ABCD – параллелограмм
; 
M
; AM : MC = 4 : 1
Найти: 
Решение:
По правилу параллелограмма
или 
Но 
, тогда 
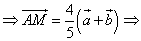
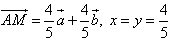
Ответ: 
***
Дано: векторы и – неколлинеарные
а) 
б) 
Найти: коэффициенты разложения x, y – ?
Решение:
а) 
3 – y = 0, x+1=0 y= 3, x= – 1
б) 
4 – x = 0, 5+y=0 x = 4, y= –5
Ответ: a) x= –1, y= 3 б) x = 4, y= –5
***
Дано: ABCD – трапеция
EF – средняя линия трапеции
Доказать: EF
AD - т.е. средняя линия трапеции параллельна её основанию, 
- т.е. длина средней линии трапеции равна полусумме основанию трапеции.
Доказательство:
По правилу многоугольника
+
Сложив оба выражения, получаем
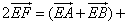
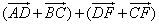
Т.к. E и F – середины сторон AB и CD, тогда
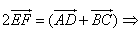
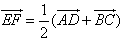
Т.к. 
, то 
, а 
Поэтому EF || AD и
Теорема: Любой вектор 
можно разложить по двум неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Дано:
вектор a, вектор b
и – неколлинеарные векторы
Доказать: 
Доказательство:
Через точку А и точку В проведем прямые, параллельные прямым, содержащих векторы и . Найдем точку С.
Тогда по правилу треугольника
Заметим, что векторы и – коллинеарные, также векторы и – коллинеарные
По лемме о коллинеарных векторах
, 
Тогда 
Единственность разложения
Доказательство:
Знаем, что (1)
Пусть есть 
(2)
В результате разности выражений (1) и (2) получаем
Это равенство возможно
; 
Т.е 
;
***
Определение: Единичным вектором называется вектор, длина которого равна единице.
i и j – координатные векторы
Т.к. 
и 
– неколлинеарные векторы, то любой вектор можно разложить через векторы и .
Т.е. 
, где x и y – координаты вектора.
{1:2}
{2:–3}
{0;0}
Если 
и 
,
то 
, если 
и 
***
Найти координаты векторов.
Решение:
{2;3}
{–2;3}
{2;0}
{–3;–4}
{2;–2}
{–4;–5}
***
Найти координаты векторов.
Решение:
{2;3}
{–;–2}
{8;0}
{1;–1}
{0;–2}
{–1;0}
***
Найти сумму вектора по его координатам.
Решение:
{–3;
} 
{–2;–3} 
{–1;0} 
{0;3} 
{0;1} 
***
Правила, позволяющие по координатам векторов находить координаты суммы, разности векторов и произведения вектора на число.
1. Суммой векторов и с координатами (a1;a2) и (b1;b2) называется вектор с координатами (a1+ b1;a2 +b2).
Дано:
{a1;a2}; {b1;b2}; 
Доказать: { a1+ b1;a2 +b2}
- сумма координат вектора, т.е. формула, как найти координаты вектора через сложение
Доказательство:
{ a1+ b1;a2 +b2}
***
Пример 1 - сложение векторов, как найти координаты векторов:
Если даны координаты векторов {3;2}; {2;5}, то
2. Разностью векторов и с координатами {a1; a2} и {b1; b2} называется вектор с координатами {a1 – b1; a2 – b2}.
3. Произведением вектора с координатами {a1; a2} на произвольное число k называется вектор с координатами {ka1; ka2}.
Дано:
{a1;a2}
k – произвольное число
Доказать: {ka1; ka2}
- умножение вектора на число
Доказательство:
Значит, вектор {ka1; ka2}
Пример 2 - как находить координаты вектора:
Найти координаты вектора 
, если
{1;2}; {0;3}; {–2;3}
Решение:
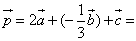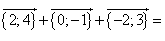{0;6}
{0;6}
Ответ: {0;6}
***
Найти координаты вектора 
, если даны векторы
{–7;–1}; {–1;7}; {4;–6}
Решение:
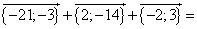
= {–21;–14}
Ответ: {–21;–14}
***
Дано:
1) 
2) 
Найти: коэффициенты разложения x, y – ?
Решение:
1)
По теореме о разложении вектора по двум неколлинеарным векторам:
x=–3, y=7
2)
По теореме о разложении вектора по двум неколлинеарным векторам:
x= –4, y=0
***
Дано: координаты векторов
1) {3;6}; {4;–3}
2) {–5;–6}; {2;–4}
Найти: разность векторов –
Решение:
1) –= 
= {–1;9}
–{–1;9}
2) –= 
={–7;–2}
–{–7;–2}
***
Дано: координаты векторов
{–2;–3}; {2;–3}; {0;5}
Найти: координаты векторов, противоположных данным.
Решение:
{–2;–3} {2;3}
{2;–3} {–2;3}
{0;5} {0;–5}
***
Дано:
Четырехугольник ABCD
M, N, K, E – середины сторон AB, BC, DC, AD
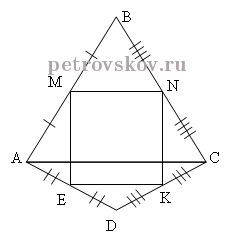
Доказать:
Четырехугольник MNKE – параллелограмм
Доказательство:
Соединим точку А и точку С.
Получим треугольник Δ ABC, где MN – средняя линия треугольника Δ ABC и треугольник Δ ADC, где EK – средняя линия треугольника Δ ADC.
По свойству средней линии треугольника Δ следует, что
MN || AC – параллельны и MN= AC,
EK || AC – параллельны и EK= AC.
Тогда MN || EK – параллельны и MN=EK, поэтому
MNKE – параллелограмм (по первому признаку параллелограмма).
Дано:
Треугольник Δ ABC
Сторона треугольника AB = 8,5 см
Сторона треугольника AC = 5 см
Высота AH = 4 см, т.е отрезок AH перпендикулярен стороне BC
H
BC, т.е. точка H лежит на стороне BC
Найти:
Площадь треугольника S ΔABC – ?
Решение:
S ΔABC = BC • AH
По теореме Пифагора
BH = 
= 
= 
= 7,5 см
По теореме Пифагора
CH = 
= 
= 3 см
BC = BH + CH = 3 +7,5 = 10,5 см
S ΔABC = • 10,5 • 4 = 21 
Ответ: S ΔABC = 21
***
Дано:
ABCD – равнобедренная трапеция
Доказать: NE KM = 
Доказательство:
Проведем перпендикуляры BH и CH1, то есть BHAD перпендикулярны; также CH1AD перпендикулярны.
Но BH и CH1 проходят через NE тогда перпендикулярны BRNE и CR1NE.
Стороны BH = CH1 равны параллельны BH || CH1
Поэтому BH = KM = CH1 равны параллельны BH KM CH1 как отрезок, заключенный между параллельными прямыми.
Следовательно углы равны 
KON = NR1C = 90° как соответственные.
ТогдаKON = EOM = 90°, как вертикальные.
***
Дано:
AB – отрезок
AC = CB
O – произвольная точка
Доказать:
Вектор OC равен половине суммы двух других векторов OA и OB, исходящих из одной и той же точки O
(1)
+
(2)
Сложив выражения (1) и (2), получаем
***
Дано:
векторы a, b, c
Три вектора 
и – неколлинеарные векторы.
Суммы и разности векторов.
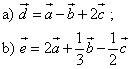
Построение:
По правилу многоугольника
a) 
б) 
=
Доказать, что отрезки, соединяющие середины противоположных сторон равнобедренной трапеции, взаимно перпендикулярны.
Дано:
четырехугольник ABCD – равнобедренная трапеция
Доказать: EF NM = , т.е. угол пересечения двух отрезков в равнобедренной трапеции равен 90°.
Доказательство:
Проведем параллельные прямые
MK || AB
MR || CD
Получим равнобедренный треугольник ΔMKR
AB=MK, так как трапеция равнобедренная,
CD=MR, т.к. трапеция равнобедренная.
Следовательно, EF – средняя линия треугольника ΔMKR, поэтому
MH=HR и OK=MO.
BM=MC=AK=RD, т.к. ABMK и MCDR – параллелограммы.
Поэтому HR=KO.
Тогда MN – медиана, биссектриса и высота равнобедренного треугольника ΔMKR.
Т.к. MN – высота, то отрезки MNAD – перпендикулярны.
По свойству средней линии треугольника Δ следует, что
EF || KR.
Тогда EF NM =
***
Доказать, что центр окружности, вписанной в равнобедренный треугольник, лежит на медиане, проведенной к основанию.
Дано:
вписанная окружность в равнобедренном треугольнике
ΔABC – равнобедренный треугольник
BH2 – медиана
Доказать: O BH2, т.е. центр вписанной окружности лежит на медиане равнобедренного треугольника
Доказательство:
Проведем перпендикуляры OH1 ; OH2 ; OH3 к сторонам BC, AC, AB.
Здесь из двух точек проведен один и тот же перпендикуляр к стороне AC, но в треугольнике можно провести только один перпендикуляр к стороне и только из одной точки.
Следовательно, что O BH2
***
Доказать, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к основанию или на ее продолжение.
Описанная окружность около равнобедренного треугольника
Δ ABC – вписанный равнобедренный треугольник
BH3 – медиана
Доказать: O BH3
Доказательство:
Проведем из центра окружности перпендикуляры
OH1 ; OH2 ; OH3 к сторонам BC, AC, AB.
Здесь проведен из двух точек перпендикуляр к стороне AC, но в треугольнике можно провести только один перпендикуляр к стороне и только из одной точки.
Следовательно, что O BH3
***