Длина окружности, площадь круга и кругового сектора

Вывод формулы длины окружности.

Пусть C и C′ - длины окружностей радиусов R и R′. Впишем в окружности правильные многоугольники.

P_n и P_n′ - их периметры, a_n и a_n′ - стороны.

P_n = n • a_n = n • 2R • Sin

P_n′ = n • a_n = n • 2R′ • Sin

Тогда

Зная, что периметры P_n и P_n′ - приближенные значения длин окружностей C и C′, при n →∞, получаем

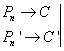
Но в силу равенства получаем

По свойству пропорции

Значение величины π ("пи") приближенно равно 3,14.

Формула длины окружности:

***

 

Задача 124.

Если известен радиус R = 4, то длина окружности C = 2πR = 2 • 3,14 • 4 = 25,12

Если C = 82, то радиус окружности R == = 13,1

Если C = 18π, то радиус окружности R == = 9

***

 

Задача 125.

Дано:

a - сторона правильного треугольника

 

Найдите: длину описанной окружности

Решение:

Т.к. сторона правильного многоугольника

a_n = 2R • Sin (), тогда сторона правильного треугольника

a = R R =

Тогда длина окружности, описанной около правильного треугольника равна C = 2πR =

***

 

Вывод формулы для вычисления дуги L с градусной мерой α.

Градусная мера окружности 360°,

Длина окружности C = 2πR

Длина дуги в 1° равна

 

 

Тогда длина дуги окружности в α градусах:

 

 

 

***

 

Задача 126.

Дано:

радиус R= 6 см,

угол дуги

1) α = 30°

2) α = 45°

3) α = 60°

4) α = 90°

 

Найти: длину дуги окружности

Решение:

1) L = • 30° = • 30° = π (см)

2) L = • 45° = • 3 = 1,5π (см)

3) L = • 60° = 2π (см)

4) L = • 90° = 3π (см)

***

 

Задача 127.

Дано:

ABCDEF - правильный шестиугольник,

площадь шестиугольника S₆ = 24 см²

 

Найти: чему равна длина описанной окружности C = ?

Решение:

C = 2πR

Значит, нужно найти радиус описанной окружности.

Площадь шестиугольника определяется по формуле

S₆ = • P₆ • r₆

Радиус вписанной окружности определяется по формуле

r₆ = R • Cos = • R

Сторона шестиугольника равна радиусу описанной окружности: a₆ = R

Тогда периметр шестиугольника P₆ = 6 • a₆ = 6R (см)

S₆ = • P₆ • r₆ = • 6R • • R = 1,5•R²

24= 1,5•R²

R² = = 16 Получаем радиус описанной окружности

R = = 4 (см)

Тогда длина описанной окружности равна

C = 2πR = 2π • 4 = 8π (см)

Ответ: 8π см.

***

 

Задача 128.

Дано:

ABCD - квадрат,

сторона квадрата AB = a

 

Найти: длину вписанной окружности C = 2π • r = ?

Решение:

r₄ = R • Cos = R • Cos 45° = R

C = 2π • r = 2π • R = π • R

AB = a = 2r = R. Значит, C = π • R= π • a

Ответ: длина окружности, вписанной в квадрат C = π • a

***

 

Задача 129.

Дано: окружность (O; R) – описанная около следующих фигур

1) Δ ABC – вписанный прямоугольный треугольник;

a, b – катеты

2) Δ ABC – вписанный равнобедренный треугольник;

a – основание, b – сторона

3) ABCD – вписанный прямоугольник,

BC = a – сторона прямоугольника,

α – острый угол между диагоналями

 

Найти: длину описанной окружности C = 2πR = ?

Решение:

1)

2R = AB R = AB

AB =

Тогда длина окружности, описанной около прямоугольного треугольника

C = 2π • • = π

 

2)

BH = =

Площадь треугольника равна половине произведения основания на высоту

S_ΔABC = BH • AC = (1)

Но площадь треугольника можно также найти через деление произведения трех его сторон на четыре радиуса описанной окружности:

S_ΔABC = = (2)

 

Используя равенства (1) и (2), получаем

= R =

 

Тогда длина окружности, описанной около равнобедренного треугольника

C = 2π •

 

3)

OB = OC = OA = OD = R

Проведем OH – высота и биссектриса равнобедренного треугольника ΔAOD.

Рассмотрим прямоугольный треугольник ΔOHD.

AOD = 180° – α,

HOD = • (180° – α)

ODA = 180° – DHO – HOD

ODA =OAD = 180° – 90° – • (180° – α) =

AH = HD =

CosOAD = Cos = =

R =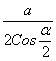

Тогда длина окружности, описанной около прямоугольника

C = 2π • =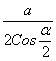

 

***

 

Площадь круга

Дано:

A₁A₂…A_n– правильный многоугольник

круг (O; R)

малый круг′ (O; r_n)

S – площадь круга

S_n′ – площадь малого круга

 

Доказать:

S = πR²

Доказательство:

Рассмотрим правильный многоугольник (см. рисунок).

Площадь круга больше площади многоугольника:

S_n < S_круга

Площадь многоугольника больше площади малого круга:

S_n′ < S_n

Тогда S_n′ < S_n < S (1)

 

Радиус окружности, вписанной в правильный многоугольник

r_n = R • Cos ()

 

При n→∞ косинус Cos ()→1, поэтому r_n → R

Следовательно, S_n′ → S при n→∞.

Из неравенства (1) следует S_n → S при n→∞.

Мы знаем, что площадь правильного многоугольника

S_n = P_n • r_n, где P_n – периметр многоугольника A₁A₂…A_n.

Учитывая, что r_n → R, P_n → 2πR, S_n → S при n→∞.

Тогда S = P_n • r_n = 2πR • R = πR²

Формула площади круга:

***

Площадь сектора круга

Определение:

Сектором круга или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

πR² – площадь круга.

Площадь кругового сектора, мера которого 1°, равна

Площадь кругового сектора, мера которого α градусов, равна

 

Формула площади сектора круга:

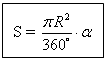, где

α – градусная мера дуги.

***

 

Задача 130.

Дано:

AOB = 72°

S – площадь кругового сектора

 

Найдите: R – радиус окружности

Решение:

S =

360° • S = πR² • α

R² = = R =

Ответ: радиус равен R =

***

Задача 131.

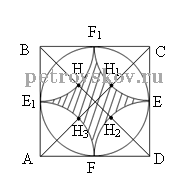
Дано:

ABCD – квадрат,

сторона квадрата AB = a

 

Вычислите:

площадь закрашенной фигуры S_EFE1F1 = ?

Решение:

S =

Рассмотрим на рисунке сектор FAE₁H₃, где AF = AH₃ = R =

S = S₁ = • 90° =

Площадь четырех секторов:

S_1+2+3+4 = 4 • =

Площадь квадрата

S_ABCD = AC • BD.

Рассмотрим ΔACD, где AD = CD = a.

По теореме Пифагора:

AC =

Тогда S_n= • = a²

Следовательно, площадь заштрихованной фигуры

S_EFE1F1 = S_ABCD – S _1+2+3+4 = a² – =

Ответ: .

***

 

Задача 132.

Дано:

окружность (O;OH₁)

окружность (O;OH₂)

окружность (O;OH₃)

окружность (O;OH₄)

OH₁ = 1, OH₂ = 2

OH₃ = 3; OH₄ = 4

 

Найти: площадь окружности (O;OH₁),

площадь каждой из трех мишеней = ?

Решение:

S_окр1 = πR² = π • (OH₁)² = π • 1 = π

S_окр2 = πR² = π • (OH₂)² = π • 4 = 4π

S_окр3 = πR² = π • (OH₃)² = π • 9 = 9π

S_окр4 = πR² = π • (OH₄)² = π • 16 = 16π

 

S_м2 = S_окр2 – S_окр1 = 4π – π = 3π

S_м3 = S_окр3 – S_окр2 = 9π – 4π = 5π

S_м4 = S_окр4 – S_окр3 = 16π – 9π = 7π

Ответ: S_окр1 = π; S_м2 = 3π; S_м3 = 5π; S_м4 = 7π.

***

 

Задача 133.

Дано:

круг (O;R), описанный около четырехугольника и треугольника

1) ABCD – прямоугольник,

a и b – стороны прямоугольника

2) Δ ABC – прямоугольный,

a – катет,

α – противолежащий угол

 

Найти: площадь круга, изображенного на рисунке.

S = πR² = ?

Решение:

1)

BD = 2BO = 2R

Рассмотрим треугольник ΔABD – прямоугольный.

По теореме Пифагора:

BD² = AB² + AD²

(2R)² = a² + b²

R² =

Тогда площадь круга S = πR² = π •

2)

Найдем площадь круга через его диаметр AB = 2AO = R

Sin α = AB =

2R = R =

 

Следовательно,

S = πR² = π • = π • =

Ответ: 1) π •; 2) .

***

 

Задача 134.

Дано:

ΔABC – прямоугольный

круг₁ (O₁; AO₁) на гипотенузе AB

круг₂ (O₂; BO₂) на катете BC

круг₃(O₃; CO₃) на катете AC

 

Доказать:

Сумма площади полукруга на гипотенузе равна сумме площадей полукругов на катетах

S₁ = S₂ + S₃

Доказательство:

Пусть AB = c; AC = a; BC = b.

Формула площади сектора круга

S =

S = =

S₁ = • O₁A², где O₁A = c S₁ =•c²

S₂ = • O₂B², где O₂B = b S₂ =•b²

S₃ = • O₃C², где O₃C = a S₃ =•a²

Тогда S₂ + S₃ =•a² +•b² = • (a² + b²)

По теореме Пифагора:

c² = a² + b²

Следовательно,

S₂ + S₃ = • (a² + b²) = • c² = S₁

Поэтому S₁ = S₂ + S₃

***

 

Задача 135.

Дано:

окружность (O; AO)

AO – радиус

AO = 10 см

AMB = AOB = 60°

 

Определите:

чему равна площадь сектора круга с дугой ALB = ?

Решение:

Градусная мера дуги

ALB = 360° – 60° = 300°

Тогда площадь сектора круга

S = = = ≈ 261,67 ≈ 262 (см²)

Ответ: площадь сегмента круга S ≈ 262 см².

***

 

Задача 136.

Дано:

круг (O; OH) вписан в ΔABC –

равносторонний

AB = a

Найти: чему равна площадь круга

S_круга = ?

Решение:

S = πR² = πr²

Рассмотрим треугольник ΔABH – прямоугольный.

AO – биссектриса угла A.

Значит, OAH = 60° : 2 = 30°

OH = AO

r =

AOH = 180° – (30° + 90°) = 60°

Sin 60° = радиус описанного круга R =

Тогда радиус вписанного круга r = : 2 =

Следовательно, площадь круга S = πr² = =

Ответ: S_круга =

***

Задача 137.

Дано:

Малый круг (O; OD)

Площадь большого круга

S _{круг(O; OC)} = 314 мм²

Диаметр малого круга

D _{круг(O; OD)} = 18,5 мм

 

Найти: разницу диаметров

HC = ?

Решение:

S = πR²

314 = πR²

= = 10 (мм)

D₂ = 2R = 2 • 9,25 = 18,5 (мм)

R₂ = 9,25 мм

HC = R₁ – R₂ = 10 – 9,25 = 0,75 (мм).

Ответ: 0,75 мм.

***

 

Задача 138.

Дано:

Малый круг (O; OH) – отверстие трубы

Радиус малой трубы OH = 3м

Разница диаметров между двумя трубами AB = 1м

На квадратный метр уходит 0,8 кубических дециметров песка

1 м² → 0,8 дм³

 

Найти: сколько нужно песка, чтобы заполнить пространство между двумя трубами

Решение:

Рассмотрим круг′ (O; OH).

Площадь данного круга:

S′ = πR² = 9 • 3,14 ≈ 28,26 (м²)

Рассмотрим круг′′ (O; OH+AB).

S′′ = πR² = 16 • 3,14 ≈ 50,24 (м²)

Тогда площадь между двумя трубами

S = S′′ – S′ = 50,24 – 28,26 ≈ 21,98 (м²)

Тогда искомое количество песка

21,98 • 0,8 ≈ 17,58 дм³ ≈ 17,6 дм³

Ответ: ≈ 17,6 дм³.

***