Теоретический урок по предмету математики для решения простейших задач в координатах.
На данной онлайн странице представлены следующие готовые домашние задания, гдз по геометрии из решебника за 9 класс:
Определение:
Радиус-вектор произвольной точки М – это вектор, проведенный из начала координат в точку М.
Теорема:
Координаты любой ![]() точки плоскости равны соответствующим координатам ее радиус-вектора.
точки плоскости равны соответствующим координатам ее радиус-вектора.
Дано:
M(x;y) – ![]() точка
точка
![]() – радиус-вектор точки М
– радиус-вектор точки М
Доказать: ![]() {x; y}
{x; y}
Доказательство:

По правилу параллелограмма ![]() , где х=OM1
, где х=OM1
![]()
![]() = OM1
= OM1![]()
![]() = x
= x![]()
![]()
![]() = OM2
= OM2![]()
![]() = y
= y![]()
Значит, ![]()

Поэтому ![]() {x; y}
{x; y}
2 случай. Если x<0
Формула для вычисления координат вектора по координатам его начала и конца.
Теорема:
Каждая координата вектора равна разности соответствующих координат его конца и начала.

![]() – произвольный вектор
– произвольный вектор
A (a1;a2) - координаты начала вектора AB
B (b1;b2) - координаты конца вектора AB
Доказать: ![]() {b1 – a1; b2 – a2}
{b1 – a1; b2 – a2}
Доказательство:
По правилу треугольника вектор ![]() =
=![]() =
=
= {b1 – a1; b2 – a2}, где ![]() {b1;b2} и
{b1;b2} и ![]() {a1;a2}, т.к. они радиус вектора.
{a1;a2}, т.к. они радиус вектора.
***
Дано:
ΔABC – равнобедренный треугольник
AB=2a, CO=h
Найти: координаты точки А, точки B и точки C
Решение:
Точка C лежит на оси ординат: С![]() Oy, то координаты точки С
Oy, то координаты точки С![]() (0;h)
(0;h)
Т.к. CO является высотой в равнобедренном треугольнике, то CO и медиана.
Следовательно, AO=OB=2a : 2 = a
Тогда координаты точки A(–a;0), координаты точки B(a;0), т.к. A и B ![]() Ox (лежат на оси абсцисс).
Ox (лежат на оси абсцисс).
***
Найти: координаты вектора ![]() , если даны координаты начала и конца вектора
, если даны координаты начала и конца вектора
1) A(2;7) и B(–2;7); 2) A(–5;1) и B(–5;27)
Решение:
1) ![]() = B–A={–2;7}–{2;7} = {–2–2;7–7}={–4;0}
= B–A={–2;7}–{2;7} = {–2–2;7–7}={–4;0}
2) ![]() = {–5;27}– {–5;1} = {–5+5;27–1}={0;26}
= {–5;27}– {–5;1} = {–5+5;27–1}={0;26}
***
Найти: координаты вектора![]() , если даны координаты начала и конца вектора
, если даны координаты начала и конца вектора
1) A(–3;0) и B(0;4); 2) A(0;3) и B(–4;0)
Решение:
1) ![]() = B–A=
= B–A= ![]()
2) ![]() = B–A=
= B–A= 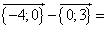
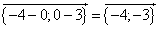
***
Найти: координаты вектора![]() , а также координаты его начала и конца вектора
, а также координаты его начала и конца вектора
Решение:
1) Если A(0;0), B(1;1), то ![]() = B–A=
= B–A= ![]()
2) Если A(x;–3), B(2;–7), ![]() {5;y}, то
{5;y}, то ![]() = B – A =
= B – A =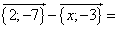
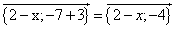
5 = 2 – x ![]() x= –3
x= –3
y = –4
3) Если A(a;b), ![]() {c;d}, то
{c;d}, то ![]() = B – A
= B – A
![]()
![]() B=
B=![]()
4) Если A(1;2), ![]() {0;0}, то
{0;0}, то ![]() = B – A
= B – A
B=![]()
***

Дано:
MNPQ – квадрат
P (–3;3) – координаты точки
NQ ∩ PM = O(0;0)
Найти: координаты точки M,N,Q
Решение:
![]()
Т.к. диагонали в квадрате в точке пересечения делятся пополам, то PO=OM ![]()
![]() , т.к. PO и OM - коллинеарные векторы, но ↑↓ – разнонаправленные.
, т.к. PO и OM - коллинеарные векторы, но ↑↓ – разнонаправленные.
Тогда ![]() {3;–3}
{3;–3}![]() M(3;–3)
M(3;–3)
Из точки P проведем перпендикуляр к оси y на пересечение с диагональю NQ.
Тогда точка N – вершина квадрата. Т.к. вершина квадрата расположена в первой (I) координатной четверти, то N(3;3); ![]()
Т.к. диагонали в точке пересечения делятся пополам, то NO=OQ ![]()
![]() , т.к. коллинеарны, но разнонаправлены ↑↓ - т.е данные векторы - коллинеарные векторы и противоположно направленные векторы
, т.к. коллинеарны, но разнонаправлены ↑↓ - т.е данные векторы - коллинеарные векторы и противоположно направленные векторы
Тогда ![]() {–3;–3}
{–3;–3} ![]() Q(–3;–3)
Q(–3;–3)
Ответ: M(3;–3), Q(–3;–3), N(3;3) и
M(3;–3), N(–3;–3), Q(3;3)
***
Каждая координата середины отрезка равна полусумме соответствующих координат его конца и начала.
Дано:
Отрезок AB, A(x1; y1), B(x2; y2)
C![]() AB, AC=CB
AB, AC=CB

Доказательство:
Т.к. вектор OC равен половине суммы двух других векторов OA и OB, исходящих из одной и той же точки O (см. Задача 4), то
![]()
Т.к. ![]() и
и ![]() являются радиус-векторами точек A и B, то
являются радиус-векторами точек A и B, то ![]() {x1; y1} и
{x1; y1} и ![]() {x2; y2}.
{x2; y2}.
Тогда 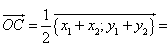
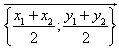
![]()
![]() C
C![]() , т.к.
, т.к. ![]() – радиус вектора точки C.
– радиус вектора точки C.
Формула, как найти координаты середины отрезка
C![]()
Пример 1.
Дано:
точки A и B – концы отрезка AB, точка M – середина отрезка AB
а) Если даны координаты точек A(2; –3); B(–3; 1), то как найти координаты середины отрезка AB
Используя формулу для нахождения координаты середины отрезка, получаем M![]()
![]() M
M![]()
![]() M
M![]()
б) Если даны координаты точек B(4; 7); M(–3; –2), то как найти координаты точки A(x;y).
![]() и
и ![]()
–6 = 4+x –4 = 7+y
x= –10 y= –11
Ответ: M![]() ; A (– 10; – 11)
; A (– 10; – 11)
***
Дано: координаты вектора
![]() {a1; a2}
{a1; a2}
Доказать: Длина вектора равна квадратному корню из суммы квадратов его координат ![]()
Доказательство:
От точки О (0;0) отложим вектор ![]() =
= ![]()
Но ![]() есть радиус-вектор точки А. Тогда A(a1; a2)
есть радиус-вектор точки А. Тогда A(a1; a2)

a1=OA1; a2=OA2=AA1
OA2=![]()
OA=![]()
Формула, как найти длину вектора по координатам вектора
![]()
Пример 2.
![]() {11;–11}, то
{11;–11}, то ![]() =
= ![]()
= ![]()
![]() {10;0}, то
{10;0}, то ![]() =
= ![]() 10
10
Дано: координаты точки
M1(x1; y1), M2(x2; y2)
Найти: расстояние между двумя точками
d= M1M2 = ?
Решение:
![]() { x2– x1; y2– y1},
{ x2– x1; y2– y1},
![]() ,
, ![]() = M1M2 = d
= M1M2 = d
Тогда ![]() –
–
Формула, как найти расстояние между двумя точками
***
Дано: координаты начала отрезка, координаты конца отрезка, координаты середины отрезка
|
| 1 | 2 | 3 | 4 |
| A | (2;–3) | ? | (0;0) | (0;1) |
| B | (–3;1) | (4;7) | (–3;7) | ? |
| M | ? | (–3;–2) | ? | (3;–5) |
Найти: координаты начала, конца и середины отрезка AB.
Решение:
Используя формулу для нахождения координаты середины отрезка, получаем M![]()
![]()
1) M![]()
![]() M(–0,5 ; –1)
M(–0,5 ; –1)
2) Если B (4;7) и M (–3;–2), то нужно найти координаты начала отрезка A(x;y) – ?
| –3= –6=4+x x=–10
| –2= –2•2=7+y y=– 11 |
3) M![]()
![]() M(–1,5 ; 3,5)
M(–1,5 ; 3,5)
4) Если A (0;1) и M (3;–5), то нужно найти координаты конца отрезка B(x;y) – ?
| 3= 6=x+0 x=6
| –5= 2•(–5)=y+1 y=– 11 |
| 5 | 6 | 7 | 8 | |
| A | (c;d) | (3;5) | (1;3) | (3t+5;7) |
| B | ? | (3;8) | ? | (t+7;–7) |
| M | (a;b) | ? | (0;0) | ? |
5) Если A (c;d) и M (a;b), то нужно найти координаты конца отрезка B(x;y) – ?
| a= 2a=c+x x=2a–c
| b= 2b=d+y y=2b–d |
6) M![]()
![]() M(3 ; 6,5)
M(3 ; 6,5)
7) Если A (1;3) и M (0;0), то нужно найти координаты конца отрезка B(x;y) – ?
| 0= 0=1+x x=–1
| 0= 0=3+y y=–3 |
8) M![]()
![]() M(2t+6 ; 0)
M(2t+6 ; 0)
***
Дано: координаты вектора
![]() {5;9};
{5;9}; ![]() {–3;4};
{–3;4}; ![]() {–10;–10};
{–10;–10}; ![]() {10;17}
{10;17}
Найти: длину векторов
![]() ;
;
![]() ;
;
![]() ;
;
![]() – ?
– ?
Решение:
Используя формулу для вычисления длины вектора по его координатам,
a) ![]() =
=![]() =
=![]() =
=![]() =
=![]()
б) ![]() =
=![]() =
=![]() =
=![]() =
=![]() =5
=5
в) ![]() =
=![]() =
=![]() =
=![]() =10
=10![]()
г) ![]() =
=![]() =
= ![]() =
= ![]()
***
Дано: координаты точек A и B
| 1 | 2 | 3 | 4 | |
| A | (2;7) | (–5;1) | (–3;0) | (0;3) |
| B | (–2;7) | (–5;–7) | (0;4) | (–4;0) |
| d | ? | ? | ? | ? |
Найти: расстояние между двумя точками – ?
Решение:
Используя формулу для вычисления расстояния между двумя точками
![]() , получаем
, получаем
1) d = ![]() =
= ![]() = 4
= 4
2) d = ![]() =
= ![]() = 8
= 8
3) d = ![]() =
=![]() =
=![]() =5
=5
4) d = ![]() =
=![]() =
=![]() =5
=5
***

система координат,
треугольник ΔABC,
AM – медиана
координаты концов треугольника
A(0;1), B(1;–4), C(5;2)
Найти: длину медианы AM– ?
Решение:
Используя формулу для нахождения координаты середины отрезка, получаем M![]()
![]() M
M![]()
![]() M(3 ; –1), т.к. точка M – середина BC
M(3 ; –1), т.к. точка M – середина BC
Используя формулу для вычисления расстояния между двумя точками
![]() , получаем
, получаем
AM =![]() =
=![]() =
=![]()
Ответ: AM =![]()
***

Дано:
OACB – параллелограмм
Длина стороны OA=a
Координаты точки B (b;c)
Найти: координаты точки C(x;y),
длину сторон AC, CO – ?
Решение:
Т.к. О – начало координат, то координаты точки О (0;0).
Т.к. OA=a и точка A лежит на оси абсцисс Ox, тогда координаты точки A (a;0).
По правилу параллелограмма и т.к. OC – вектор, то
![]()
![]()
![]() =
=![]()
Таким образом, вектор ![]() имеет координаты {a+b;c}
имеет координаты {a+b;c}
Т.к. ![]() – радиус-вектора точки C, то координаты точки C (a+b;c).
– радиус-вектора точки C, то координаты точки C (a+b;c).
Используя формулу для вычисления расстояния между двумя точками
![]() , получаем
, получаем
AC =![]() =
=![]()
CO = ![]() =
=![]() =
=![]()
Ответ: C (a+b;c) ; AC=![]() ; CO =
; CO = ![]()
***

Дано:
система координат,
треугольник ![]() ,
,
координаты концов треугольника A(0;1), B(1;–4), C(5;2)
1) Доказать: треугольник ΔABC - равнобедренный
Доказательство:
Используя формулу для вычисления расстояния между двумя точками
![]() , получаем
, получаем
AC=![]() =
=![]() =
=![]()
AB=![]() =
=![]() =
=![]()
Т.к. AC=AB=![]() , то треугольник ΔABC – равнобедренный.
, то треугольник ΔABC – равнобедренный.
2) Найти: SΔABC площадь треугольника ΔABC – ?
Решение:
Проведем высоту AM к основанию BC.
Используя формулу для вычисления площади треугольника, получаем
SΔABC=![]() AM•BC
AM•BC
Используя формулу для нахождения координаты середины отрезка, получаем M![]()
![]() M
M![]()
![]() M(3 ; –1), т.к. точка M – середина BC
M(3 ; –1), т.к. точка M – середина BC
Используя формулу для вычисления расстояния между двумя точками
![]() , получаем
, получаем
AM =![]() =
=![]() =
=![]()
BC =![]() =
=![]() =2
=2![]()
Тогда площадь треугольника SΔABC =![]() •
•![]() •2
•2![]() =
=![]() =13
=13

***
Дано:
система координат,
треугольник ΔMNP,
координаты вершин треугольника
M(4;0), N(12;–2), P(5;–9)
Найти: периметр треугольника PΔMNP – ?
Решение:
Используя формулу для вычисления расстояния между двумя точками
![]() , получаем
, получаем
MN=![]() =
=![]() =
=![]() =
=![]()
NP=![]() =
=![]() =
=![]()
PM=![]() =
=![]() =
=![]()
Используя формулу для вычисления периметра треугольника, получаем PΔMNP =MN+NP+PM=![]() +
+![]() +
+![]()
Ответ: PΔMNP =![]() +
+![]() +
+![]()
***

Дано:
MNPQ – четырехугольник
координаты вершин четырехугольника
M(1;1), N(6;1), P(7;4), Q(2;4)
1) Доказать: MNPQ – параллелограмм
Доказательство:
Используя формулу для вычисления расстояния между двумя точками
![]() , получаем
, получаем
MN=![]() =
=![]() = 5
= 5
PQ =![]() =
=![]() = 5
= 5
NP =![]() =
=![]() =
= ![]()
QM =![]() =
=![]() =
= ![]()
Т.к. MN=PQ=5 и NP=QM=![]() , то MNPQ – параллелограмм
, то MNPQ – параллелограмм
2) Найти: длину MP, NQ – ?
Решение:
Используя формулу для вычисления расстояния между двумя точками
![]() , получаем
, получаем
MP =![]() =
=![]() =
= ![]() =
=![]() =3
=3![]()
NQ =![]() =
=![]() =
= ![]() = 5
= 5
Ответ: MP= 3![]() , NQ = 5
, NQ = 5
***
Дано:
координаты точек C(4;–3), D(8;1)
точка А лежит на оси ординат Oy
AC=AD
Найти: координаты точки A – ?
Решение:
1) Т.к. точка A лежит на оси ординат Oy, то ее координаты (0;y).
2) Используя формулу для вычисления расстояния между двумя точками ![]() , получаем
, получаем
AD=![]() =
=![]()
3) AC=![]() =
=![]()
4) Т.к. AC=AD, то ![]() =
=![]()
64 + (y – 1)2= 16 + (3 + y)2
64 + 1 – 2y+y2=16 + 9 + 6y + y2
–2y – 6y= 25 – 65
–8y = –40
y = 5
Ответ: A (0; 5).
***
Дано:
O(0;0)
ΔABC – равнобедренный
Медиана OC=160см

Найти: AK; NB
Решение:
1) Т.к. точки A и B лежат на оси абсцисс Ox,
AO=OB=80 : 2 = 40 (см) ![]()
Координаты точек B(40;0) и A(–40;0)
2) Т.к. OC = 160 см и точка C лежит на оси ординат Oy![]()
Координаты точки C(0;160)
3) Т.к. K – середина BC, то, используя формулу для нахождения координаты середины отрезка, получаем K![]()
![]()
K![]()
![]() K(20 ; 80)
K(20 ; 80)
4) Тогда, используя формулу для вычисления расстояния между двумя точками ![]() , получаем
, получаем
AK= ![]() =
= ![]() =
=![]() =100 (см)
=100 (см)
5) Т.к. N – середина отрезка AC, то, используя формулу для нахождения координаты середины отрезка, получаем
N![]()
![]() N
N![]()
![]() N(–20 ; 80)
N(–20 ; 80)
6) Используя формулу для вычисления расстояния между двумя точками ![]() , получаем
, получаем
NB = ![]() =
= ![]() =
=![]() =100 (см)
=100 (см)
Ответ: AK = NB = 100 см
***

Дано:
Треугольник ΔABC
Прямой угол ![]() C = 90°
C = 90°
Точка M лежит на стороне AB
Точка M – середина стороны AB
BC=a, AC=b
Доказать: длина высоты в прямоугольном треугольнике равна половине длины гипотенузы.
Доказательство:
Т.к. BC=a, AC=b, то
точка C (0;0) – т.к. точка C – начало координат
Тогда B(a;0), A(0;b).
Используя формулу для нахождения координаты середины отрезка, получаем M![]()
![]() M
M![]()
![]() M(
M(![]() ;
;![]() ), т.к. точка M – середина AB.
), т.к. точка M – середина AB.
Используя формулу для вычисления расстояния между двумя точками ![]() , получаем
, получаем
MC=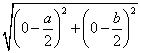 =
= 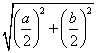 =
=![]()
AM=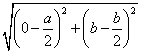 =
= ![]()
Следовательно, AM=MB=MC.
***

Дано:
ABCD – параллелограмм
AD=BC=a
координаты точек
B(b;c), D(a;0), C(a+b;c)
Доказать:
Сумма квадратов сторон параллелограмма равна сумме квадратов отрезков, соединяющих противоположные вершины параллелограмма.
AB2 + BC2 + CD2 + AD2 = AC2 + BD2
Доказательство:
используя формулу для вычисления расстояния между двумя точками ![]() , получаем
, получаем
AB=![]()
![]() AB2 = b2+c2
AB2 = b2+c2
AD=![]()
![]() AD2 = a2
AD2 = a2
AC=![]()
![]() AC2 = (a+b)2 + c2
AC2 = (a+b)2 + c2
BD=![]()
![]() AC2 = (a–b)2 + c2
AC2 = (a–b)2 + c2
Т.к. AB=CD, AD=BC, тогда
AB2 + AD2 + BC2 + CD2 = 2(AB2 + AD2) = 2(b2+c2 + a2)
AC2 + BD2 = (a+b)2 + c2 + (a–b)2 + c2 = a2 + 2ab + b2 + c2 + a2 – 2ab + b2 + c2 = 2(a2 + b2 + c2)
Т.е. AB2 + BC2 + CD2 + AD2 = AC2 + BD2
***

Определение: Уравнение с двумя переменными x и y называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии L, и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

Теорема - формула уравнения окружности или уравнения радиуса окружности:
В прямоугольной системе координат уравнение окружности с центром в точке C(x0; y0) и радиуса – r имеет вид
(x – x0)2 + (y – y0)2 = r 2
Дано:
Окружность (C;r) с центром в точке C,
координаты точки C(x0; y0)
Доказать: уравнение окружности (x – x0)2 + (y – y0)2 = r 2
Доказательство:
Возьмем точку M(x;y), лежащей на окружности (C;r)
Используя формулу для вычисления расстояния между двумя точками ![]() , получаем
, получаем
CM=![]() , но CM=r
, но CM=r
Тогда CM2 = r2 ![]()
r2 = (x – x0)2 + (y – y0)2 (1)
Координаты точки M удовлетворяют уравнению (1).
Если N(x1;y1) не лежит на окружности (C;r), тогда
Т.к. NC ≠ r , то координаты точки N не удовлетворяют уравнению (1).
Значит, уравнение окружности (x – x0)2 + (y – y0)2 = r 2
Если центр окружности – точка C имеет координаты C(x0; y0) = O(0;0) ![]() уравнение окружности x2 + y2 = r 2
уравнение окружности x2 + y2 = r 2
***

Дано: уравнение окружности с центром в точке A, проходящей через 2 точки
а) x2 + y2 = 9
б) (x – 1)2 + (y + 2)2 = 4
в) (x + 5)2 + (y – 3)2 = 25
г) (x – 1)2 + y2 = 4
д) x2 + (y + 2)2 = 2
Найти: центр окружности и ее радиус r
Решение:
а) Пусть существует окружность с центром A и радиусом r или кратко:
окр(A;r),
а также точка B c координатами (x;y), которая лежит на данной окружности или кратко:
B(x;y)![]() окр.
окр.

Т.к. x2 + y2 = 9, то x0 =0 и y0=0, тогда центр окружности имеет координаты A(0;0). График окружности представлен на рисунке а).
б) Т.к. (x – 1)2 + (y + 2)2 = 4, то по уравнению окружности ![]()
x0 = 1 и y0= – 2.
Тогда A(1;–2), где A – центр окружности.
Т.к. r2 = 4, то r = 2. График окружности представлен на рисунке б)
в) Т.к. (x + 5)2 + (y – 3)2 = 25, то по уравнению окружности ![]()

Тогда A(–5;3), где A – центр окружности.
Т.к. r2 = 25, то r = 5.
Изобразим данную окружность. График окружности представлен на рисунке в)
г) Т.к. (x – 1)2 + y2 = 4, то по уравнению окружности
![]()

Тогда A(1;0), где A – центр окружности.
Т.к. r2 = 4, то r = 2.
Изобразим данную окружность. График окружности представлен на рисунке г)
д) Т.к. x2 + (y + 2)2 = 2, то по уравнению окружности
![]()

Тогда A(0;–2), где A – центр окружности.
Т.к. r2 = 2, то r ≈ 1,4.
Изобразим данную окружность. График окружности представлен на рисунке д)
***
Дано: окружность задана уравнением
а) x2 + y2 = 25
б) (x – 1)2 + (y + 3)2 = 9
Определить: какие из точек A,B,C,D,E принадлежат окружности (A;r)
Если A(3;–4); B(1;0); C(0;5); D(0;0); E(0;1)
Решение:
а) Если A(3;–4), где x=3 и y=–4, то 32 + (–4)2 = 25
9+16=25
25=25
Точка A принадлежит окружности (A;r) или т.A![]() окр (A;r)
окр (A;r)
Если B(1;0), где x=3 и y=0, то 12 + 02 = 25
1≠25
Значит, точка B не принадлежит окружности (A;r) или т.B![]() окр (A;r)
окр (A;r)
Если C(0;5), где x=0 и y=5, то 02 + 52 = 25
25=25
Значит, точка C принадлежит окружности (A;r) или т.C![]() окр (A;r)
окр (A;r)
Если D(0;0), где x=0 и y=0, то 02 + 02 = 25
0≠25
Значит, точка D не принадлежит окружности (A;r) или т.D![]() окр (A;r)
окр (A;r)
Если E(0;1), где x=0 и y=1, то 02 + 12 = 25
1≠25
Значит, точка E принадлежит окружности (A;r) или т.E![]() окр (A;r)
окр (A;r)
б) Если A(3;–4), где x=3 и y=–4, то (3 – 1)2 + (–4 + 3)2 = 9
4+1=9
5≠9
Точка A не принадлежит окружности (A;r) или т.A![]() окр (A;r)
окр (A;r)
Если B(1;0), где x=1 и y=0, то (1 – 1)2 + (0 + 3)2 = 9
9=9
Точка B принадлежит окружности (A;r) или т.B![]() окр (A;r)
окр (A;r)
Если C(0;5), где x=0 и y=5, то (0 – 1)2 + (5 + 3)2 = 9
1+64≠9
65≠9
Точка C не принадлежит окружности (A;r) или т.C![]() окр (A;r)
окр (A;r)
Если D(0;0), где x=0 и y=0, то (0 – 1)2 + (0 + 3)2 = 9
10≠9
Точка D не принадлежит окружности (A;r) или т.D![]() окр (A;r)
окр (A;r)
Если E(0;1), где x=0 и y=1, то (0 – 1)2 + (1 + 3)2 = 9
17≠9
Точка E не принадлежит окружности (A;r) или т.E![]() окр (A;r)
окр (A;r)
***
Дано: окружность, заданная уравнением
Уравнение окружности через 2 точки (x+5)2 + (y – 1)2 = 16
Окружность (C;r), где r=4, C(–5;1)
Точка A(–2;4), B(–5;–3)
Определить: какие из точек A или B принадлежат окружности (C;r)
Решение:
Используя формулу для вычисления расстояния между двумя точками ![]() , получаем
, получаем
CA=![]() =
=![]() =3
=3![]() ,
,
3![]() >4, значит, точка A – снаружи окружности (C;r)
>4, значит, точка A – снаружи окружности (C;r)
CB=![]() =
=![]() =4,
=4,
4=4, значит, точка B лежит на окружности (C;r)
***
Дано:
Окружность (C;r), где диаметр окружности d=MN
Координаты точек M(–3;5), N(7;–3)
Напишите: уравнение окружности с центром C, проходящей через 2 точки - M и N
Решение:
Используя формулу для вычисления расстояния между двумя точками ![]() , получаем
, получаем
CA=![]() =
=![]() =
=![]() =2
=2![]() ,
,
Т.к. d=2r, то r =![]() • d =
• d = ![]() =
=![]()
Используя формулу для нахождения координаты середины отрезка, получаем координаты центра окружности C![]()
![]() C
C![]()
![]() C(2;1), т.к. точка C – середина MN.
C(2;1), т.к. точка C – середина MN.
Используя формулу уравнения окружности (x – x0)2 + (y – y0)2 = r 2, следовательно, (x – 2)2 + (y – 1)2 = ![]()
(x – 2)2 + (y – 1)2 = 41
Ответ: (x – 2)2 + (y – 1)2 = 41
***
Дано:
Окружность (C;r), где координаты центра окружности C(0;y)
Точки A и B лежат на окружности
Координаты точек A(–3;0), B(0;9)
Написать: уравнение окружности с центром в точке C, проходящей через 2 точки
Решение:
Используя формулу уравнения окружности (x – x0)2 + (y – y0)2 = r 2, следовательно, x2 + (y – y0)2 = r 2
Т.к. точка B лежит на окружности и ее координаты B(x=0;y=9).
Тогда точка B лежит на оси ординат Oy, то CB=r.
x2 + (y – y0)2 = r 2 ![]() 02+ (9 – y0) 2 = r 2
02+ (9 – y0) 2 = r 2
Т.к. точка A лежит на окружности и ее координаты
A(x=–3;y=0).
Тогда точка A лежит на оси абсцисс Ox, то CB=r.
(–3)2 + (0 – y0)2 = r 2 ![]() 9 + y02 = r 2
9 + y02 = r 2
Тогда (9 – y0) 2 = 9 + y02
y0 2 – 18 y0 + 81 = 9 + y02
– 18 y0 = – 72
y0 = 4
Значит, C(0;4).
Получаем уравнение окружности вида x2 + (y – 4)2 = r 2
Найдем радиус r.
Т.к. точки A и B принадлежат окружности, то
| (–3)2 + (0 – 4)2 = r2 9+16 = r2 r2 = 25 | или | 02 + (9 – 4)2 = r2 r2 = 25
|
Отсюда следует уравнение окружности x2 + (y – 4)2 = 25
Ответ: x2 + (y – 4)2 = 25
***
График уравнения прямой линии, проходящей через точку. Виды уравнений прямой.
1) Формула уравнения прямой l: ax + by + c = 0, где a,b,c – коэффициенты уравнения прямой | |||
2) l1: y = y0 – уравнение прямой, проходящей через точку M0, перпендикулярной прямой y, оси ординат Oy, параллельно прямой x, оси абсцисс Ox | |||
3) l2: x = x0 – уравнение прямой, проходящей через точку M0, параллельной прямой оси ординат Oy, перпендикулярно оси абсцисс Ox | |||
| 4) y = 0 уравнение прямой, оси абсцисс Ox, проходящей через начало координат 5) x = 0 уравнение оси ординат Oy, которая проходит через точку начала координат  |
Составить: уравнение прямой, проходящей через 1 точку – центр окружности.
а) (x +3)2 + (y – 2)2 = 25, параллельно оси Oy
б) (x –2)2 + (y +5)2 = 3, параллельно оси Ox
Решение:
а) (x +3)2 + (y – 2)2 = 25 ![]() центр окружности окр(–3;2), где r=5
центр окружности окр(–3;2), где r=5
Прямая проходит параллельно оси Oy , тогда ее уравнение x=x0.
Значит, x= –3.
б) (x – 2)2 + (y +5)2 = 3 ![]() центр окружности окр(2;–5), где r=
центр окружности окр(2;–5), где r=![]()
Прямая проходит параллельно оси Oy , тогда ее уравнение y=y0.
Значит, y= –5.
***
Дано: уравнения двух прямых
b1: 4x + 3y – 6=0
прямая b2 задана уравнением: 2x + y – 4=0
Укажите: координаты A(x;y), где A – точка пересечения прямых b1 и b2
Решение:
Составим и решим систему уравнений прямых
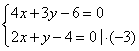
![]()
![]()
![]()
Сумма уравнений (1) и (2) ![]() –2x = –6
–2x = –6
Тогда x=3.
Подставим x=3 в уравнение 4x+3y=6.
Тогда 12+3y= –6 ![]() y= –2
y= –2
Ответ: A(3; –2)
***
Дано: координаты двух точек A(1;–1), B(–3;2)
Найдите: уравнение прямой AB по точкам
Решение:
Общее уравнение прямой имеет вид AB=ax+by+c=0, где через координаты нужно найти a=? b=? c=?
Т.к. точки A и B лежат на прямой AB (или кратко: A и B![]() пр. AB),
пр. AB),
то их координаты удовлетворяют уравнению прямой AB
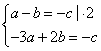
![]()
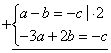
![]()
–a=–3c ![]() a=3c
a=3c
Тогда в уравнение a–b=–c подставим a=3c. Значит,
3c–b=–c
–b=–4c
b=4c
Тогда уравнение прямой AB через две точки: ax+by+c=0
3c+4cy+c=0
c(3x+4y+1)=0
3x+4y+1=0
Ответ: уравнение прямой по двум данным точкам 3x+4y+1=0
***
Дано: координаты двух точек C(2;5), D(5;2)
Составьте: уравнение прямой AB, проходящей через 2 заданные точки
Решение:
Общее уравнение прямой AB: ax+by+c=0, где нужно найти a=? b=? c=?
Т.к. точки A и B лежат на прямой AB, то следовательно их координаты удовлетворяют уравнению прямой AB
![]()
![]()
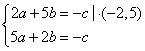
![]()
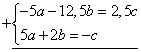
![]()
–10,5b=1,5c
c=–7b
Тогда в уравнение 2a+5b=–c подставим
c=–7b, значит, 2a+5b=7b
2a=7b–5b
a=b
Тогда следует записать уравнение прямой AB: ax+by+c=0
bx+by+(–7b)=0
b(x + y – 7)=0
x + y – 7=0
Ответ: по указанным двум точкам следует задать уравнение прямой AB x+y–7=0
***
Дано:
прямая AB задается уравнением 3x–4y+12=0
Найти: координаты двух точек A и B – точки пересечения с осями координат
Решение:
Т.к. точки A и B лежат на прямой AB, то следовательно их координаты удовлетворяют уравнению прямой AB.
Т.к. прямая AB пересекает с осями координат, то
I координата – (x;0)
II координата – (0;y)
Значит, 3x–4•0+12=0

x=–4 ![]() A(–4;0)
A(–4;0)
3•0–4y+12=0
–4y=–12
y=3 ![]() B(0;3)
B(0;3)
Далее следует построить прямую AB в координатной плоскости.
Для построения прямой сначала отмечаем точки в системе координат: абсцисса точки A равна -4, ее ордината равна нулю; абсцисса точки B равна нулю, ее ордината равна 3. Проводим прямую линию через отмеченные две точки.
Ответ: A(–4;0), B(0;3)
***
Дано:
Треугольник ΔABC
Координаты вершин треугольника A(4;6), B(–4;0), C(–1;–4)
Точка M лежит на отрезке AB
Запишите: по координатам точек уравнение прямой линии, содержащей медиану MC
Решение:
Найдем координату точки M.
Используя формулу для нахождения координаты середины отрезка, получаем M![]()
![]() M
M![]()
![]()
M(0;3), т.к. точка M – середина AB.
Каноническое уравнение прямой MC, проходящей через точку, имеет вид: ax+by+c=0, где нужно найти a=? b=? c=?
Т.к. точки M и C лежат на прямой MC (или кратко: M,C![]() MC), то, следовательно их координаты удовлетворяют уравнению прямой MC.
MC), то, следовательно их координаты удовлетворяют уравнению прямой MC.
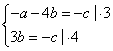
![]()
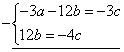
![]()
–3a=–7c![]()
![]()
Подставив ![]()
в уравнение –a – 4b = –c, получаем
![]()
![]()
![]()
![]()
![]()
![]() b=
b=![]()
Зная a и b, найдем координатное уравнение прямой MC: ax+by+c=0
![]()
![]()
![]()
![]()
![]() 7x–y+3=0
7x–y+3=0
Ответ: линейное уравнение прямой MC: 7x–y+3=0
***