Теоретический урок для решения задач по теме "Решение треугольников". Бесплатное обучение.
Содержание данной онлайн страницы электронного справочника по предмету математики для школьников:

Треугольник ΔABC,
стороны треугольника a=10, b=7
Угол ![]() A = 60°
A = 60°
Решить треугольник: Угол по сторонам треугольника ![]() B,
B, ![]() C, сторону c
C, сторону c
Решение:
Известно, что формула синуса
![]() , получаем выражение
, получаем выражение
Sin B = ![]() =
= ![]() =
= ![]() =
= ![]() ≈ 0,6062
≈ 0,6062
Используя Sin B ≈ 0,6062, находим из тригонометрической таблицы ("Четырехзначные математические таблицы" Владимира Модестовича Брадиса)
![]() B = 37°19’
B = 37°19’
Тогда ![]() C = 180° - (60° + 37°19’) = 82°41’
C = 180° - (60° + 37°19’) = 82°41’
Используя теорему синусов
![]() , получаем равенство
, получаем равенство
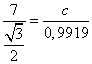
![]() с=
с=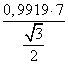 ≈ 11
≈ 11
Ответ: ![]() B = 37°19’;
B = 37°19’; ![]() C = 82°41’; c ≈ 11
C = 82°41’; c ≈ 11
***
Дано:
Треугольник ΔABC, стороны треугольника
a=6,3
b=6,3

Найти: Угол по сторонам треугольника ![]() A,
A, ![]() B, сторону c
B, сторону c
Решение:
Т.к. a=b=6,3, то треугольник ΔABC - равнобедренный.
Тогда ![]() A =
A =![]() B = (180° - 54°): 2 = 63°
B = (180° - 54°): 2 = 63°
Используя теорему синусов
![]() , получаем равенство
, получаем равенство
![]()
![]() с =
с = ![]() =
= ![]() ≈ 5,7
≈ 5,7
Ответ: ![]() A =
A =![]() B = 63°; с ≈ 5,7
B = 63°; с ≈ 5,7
***
Дано:
Треугольник ΔABC
![]() A = 60°
A = 60°

c=14
Найти: угол треугольника ![]() C, стороны a,b
C, стороны a,b
Решение:
![]() C = 180° - (40° + 60°) = 80°
C = 180° - (40° + 60°) = 80°
Используя теорему синусов
![]() , получаем выражение
, получаем выражение
![]()
![]() a =
a = ![]() ≈ 12
≈ 12
![]()
![]() b =
b = ![]() ≈ 9
≈ 9
Ответ: ![]() C = 80°; a ≈ 12; b ≈ 9
C = 80°; a ≈ 12; b ≈ 9
***

Треугольник ΔABC
BC=a=6
AC=b=7,3
AB=c=4,8
Найти: углы треугольника ![]() A,
A, ![]() B,
B, ![]() C по сторонам
C по сторонам
Решение:
Известно, что формула косинуса
![]() , находим косинус угла B
, находим косинус угла B
Cos B = ![]() =
= ![]() =
= ![]() =
= ![]() ≈ 0,0998263
≈ 0,0998263
Используя тригонометрические таблицы ("Четырехзначные математические таблицы" В. М. Брадиса), находим значение угла B
![]() B = 84°16’
B = 84°16’
Используя формулу теоремы косинусов, находим косинус угла C
Cos C = ![]() =
= ![]() =
=
= ![]() ≈ 0,7562785
≈ 0,7562785
Используя тригонометрические таблицы ("Четырехзначные математические таблицы" В. М. Брадиса), находим значение угла C
![]() C = 40°52’
C = 40°52’
Тогда угол A равен ![]() A =180° - (40°52’ + 84°16’) = 54°52’
A =180° - (40°52’ + 84°16’) = 54°52’
Ответ: ![]() A = 54°52’ ;
A = 54°52’ ; ![]() C = 40°52’ ;
C = 40°52’ ; ![]() B = 84°16’
B = 84°16’
***
Дано:
Треугольник ΔABC
![]() A = 30°
A = 30°
![]() C = 75°
C = 75°
b = 4,5
Найти: угол ![]() B, стороны треугольника a,c
B, стороны треугольника a,c
Решение:
![]() B = 180° - (30° + 75°) = 75°
B = 180° - (30° + 75°) = 75°
Т.к. два угла в треугольнике равны ![]() B =
B =![]() C = 75°, тогда треугольник ΔABC - равнобедренный.
C = 75°, тогда треугольник ΔABC - равнобедренный.
Значит, две стороны равны AC=AB=b=c=4,5
Используя теорему синусов
![]() ,
,
находим сторону BC=a
![]()
![]() a =
a = ![]() ≈ 2,3
≈ 2,3
Ответ: ![]() B = 75°; a ≈ 2,3 ; c = 4,5
B = 75°; a ≈ 2,3 ; c = 4,5
***
Дано:
Треугольник ΔABC, длины трех его сторон
| 1) a=5 , b=c=4 | 2) a=5 , b=9 , c=6 | 3) a=17 , b=15 , c=8 |
Найти: является ли треугольник тупоугольным, прямоугольным, остроугольным
Решение:
1) Т.к. b=c=4, то треугольник ΔABC - равнобедренный, и, значит, остроугольный.

![]() , находим косинус угла A
, находим косинус угла A
Cos A = ![]() =
= ![]() =0
=0
Тогда угол A равен ![]() A = 90°. Следовательно, треугольник ΔABC - прямоугольный.
A = 90°. Следовательно, треугольник ΔABC - прямоугольный.
3) Используя формулу теоремы косинусов
![]() , находим косинус угла B
, находим косинус угла B
Cos B = ![]() =
=![]() = -
= -![]() < 0.
< 0.
Т.к. значение косинуса угла B меньше нуля, следовательно, угол B - тупой, а треугольник ΔABC - тупоугольный.
***

Треугольник ΔABC, два угла и сторона
![]() A = 45°
A = 45°
![]() C = 30°
C = 30°
AD = 3 м
Найти: длину всех сторон треугольника ΔABC = ?
Решение:
Зная размер двух углов в треугольнике ΔABC, находим третий угол![]() B = 180° - (30° + 45°) = 105°
B = 180° - (30° + 45°) = 105°
Найдем угол ![]() DAB и рассмотрим ΔADC
DAB и рассмотрим ΔADC
![]() DAB = 180° - (90° + 45 + 30°) = 15°
DAB = 180° - (90° + 45 + 30°) = 15°
![]() DAC = 15° + 45° = 60°
DAC = 15° + 45° = 60°
Используя теорему синусов
![]() , находим сторону AC
, находим сторону AC
![]()
![]()
AC = (3 • 1) • 2 = 6 (м)
Используя теорему синусов
![]() , находим сторону AB
, находим сторону AB
![]()
![]()
AB = ![]() ≈ 3 (м)
≈ 3 (м)
Используя теорему синусов
![]() , находим сторону BC
, находим сторону BC
![]()
![]() BC =
BC =![]() ≈ 4 (м)
≈ 4 (м)
Ответ: AB ≈ 3 м, AC = 6 м, BC ≈ 4 м.
***

Дано:
Треугольник ΔABC
Три стороны a = 14, b = 18,
c = 20
Найти:
все углы треугольника ΔABC = ?
Решение:
Т.к. против большего угла лежит большая сторона, то используя формулу теоремы косинусов
Cos C =![]() , находим косинус угла C
, находим косинус угла C
Cos C = ![]() =
= ![]() ≈ 0,24
≈ 0,24
Используя тригонометрические таблицы ("Четырехзначные математические таблицы" В. М. Брадиса), находим приближенное значение угла C
![]() C ≈ 76°07’
C ≈ 76°07’
Используя формулу теоремы косинусов
Cos B =![]() , находим косинус угла B
, находим косинус угла B
Cos B = ![]() =
=![]() =
=![]() ≈ 0,4857
≈ 0,4857
Используя тригонометрические таблицы ("Четырехзначные математические таблицы" В. М. Брадиса), находим приближенное значение угла B
![]() B ≈ 60,941 ≈ 60°57’
B ≈ 60,941 ≈ 60°57’
Следовательно, ![]() A = 180° - (76°13’ + 60°57’) ≈ 42°56’
A = 180° - (76°13’ + 60°57’) ≈ 42°56’
Ответ: ![]() A ≈ 42°56’ ;
A ≈ 42°56’ ; ![]() B ≈ 60°57’ ;
B ≈ 60°57’ ; ![]() C ≈ 76°07’
C ≈ 76°07’
***

Дано:
Треугольник ΔEKP, сторона и два угла
EP = 0,75
![]() P = 40°
P = 40°
![]() K = 25°
K = 25°
Найти: сторону треугольника PK = ?
Решение:
Используя теорему синусов
![]() , находим сторону PK
, находим сторону PK
![]() E = 180° - (40° + 25°) =115°
E = 180° - (40° + 25°) =115°
Sin 115° = Sin (180° - 65°) = Sin 65°
Тогда ![]()
![]()
![]()
![]()
![]() PK =
PK = ![]() ≈ 1,61
≈ 1,61
Ответ: PK ≈ 1,61.
***
Дано:
Треугольник ΔABC, две стороны и угол
b = 18, c = 12
![]() A = 50°
A = 50°
Найти: решить треугольник - определить значение стороны и двух углов
(a, ![]() B,
B, ![]() C ) = ?
C ) = ?
Решение:
Используя формулу теоремы косинусов
![]() , получаем
, получаем
a = ![]() =
= ![]() ≈ 13,8
≈ 13,8
Используя формулу теоремы косинусов
Cos C =![]() , находим косинус угла C
, находим косинус угла C
Cos C =![]() =
= ![]() ≈ 0,7457
≈ 0,7457
Используя тригонометрические таблицы ("Четырехзначные математические таблицы" В. М. Брадиса), находим приближенное значение угла C
![]() C ≈ 41°47’
C ≈ 41°47’
Следовательно, ![]() B = 180° - (50° + 41°47’) ≈ 88°13’
B = 180° - (50° + 41°47’) ≈ 88°13’
Ответ: a ≈ 13,8 ; ![]() B ≈ 88°13’ ;
B ≈ 88°13’ ; ![]() C ≈ 41°47’
C ≈ 41°47’
***