Solving Triangles

Problem 76.

Given:

The triangle ΔABC,

the sides of the triangle a=10, b=7

the angle A = 60°

Solve a triangle: B, C - the angles between the triangle sides,

- the length of the side c

Solution:

It is known that the sine formula

, we obtain the expression

Sin B = = = = ≈ 0.6062

Using Sin B ≈ 0.6062 and the trigonometric table of the book "The four-valued mathematical tables" or the calculation on the smartphone/ mobile phone: function "scientific calculator" – option "DEG" – button "SIN^-1" – enter "0.6062" – button ")" – on the screen "asin(0.6062)" – button "=" – on the screen "37.315"

37.315° = 37° + 0.315 • 60’ = 37°19’

B = 37°19’

Then C = 180° - (60° + 37°19’) = 82°41’

Using the law of sines

, we obtain the equality

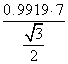c=≈ 11

 

Answer: B = 37°19’; C = 82°41’; c ≈ 11

***

 

Problem 77.

Given:

the triangle ΔABC, the sides of the triangle

a=6.3

b=6.3

C = 54°

Find: A, B - the angles between the sides of the triangle,

the length of the side c

Solution:

Since a=b=6.3, we see that the triangle ΔABC - is isosceles.

Then A =B = (180° - 54°): 2 = 63°

Using the law of sines

, we obtain the equality

c = = ≈ 5.7

Answer: A =B = 63°; c ≈ 5.7

***

 

Solving triangles having used the sine and the cosine of the angle

Problem 78.

Given:

the triangle ΔABC

A = 60°

B = 40°

c=14

Find: C - the angle of the triangle, the lengths of the sides a,b

Solution:

C = 180° - (40° + 60°) = 80°

Using the law of sines

, we obtain the expression

a = ≈ 12

b = ≈ 9

Answer: C = 80°; a ≈ 12; b ≈ 9

***

 

Problem 79.

Given:

the triangle ΔABC

BC=a=6

AC=b=7.3

AB=c=4.8

 

Find: A, B, C - the angles of the triangle

Solution:

It is known that the cosine formula

, so we find the cosine of the angle B

Cos B = = = = ≈ 0.0998263

Using the calculation’s results on the scientific calculator, we find the value of the angle B

B = 84°16’

Using the formula of the law of cosines, we find the cosine of the angle C

Cos C = = =

= ≈ 0.7562785

Using the calculation’s results on the scientific calculator, we find the value of the angle C

C = 40°52’

Then the angle A A =180° - (40°52’ + 84°16’) = 54°52’

Answer: A = 54°52’ ; C = 40°52’ ; B = 84°16’

***

 

Problem 80.

Given:

the triangle ΔABC

A = 30°

C = 75°

b = 4.5

 

Find: the angle B, the sides of the triangle a,c

Solution:

B = 180° - (30° + 75°) = 75°

Since two angles in the triangle are equal B =C = 75°, we see that the triangle ΔABC - is isosceles.

Therefore, the two sides are equal AC=AB=b=c=4.5

Using the law of sines

,

we find the side BC=a

a = ≈ 2.3

Answer: B = 75°; a ≈ 2.3 ; c = 4.5

***

 

Problem 81.

Given:

the triangle ΔABC, the lengths of its sides

 

1) a=5 , b=c=4

2) a=5 , b=9 , c=6

3) a=17 , b=15 , c=8

 

Find: whether the triangle is obtuse, right, acute

Solution:

1) Since b=c=4, we see that the triangle ΔABC - is isosceles, and therefore acute.

 

2) Using the formula of the law of cosines

, we find the cosine of the angle A

Cos A = = =0

Then the angle A is A = 90°. Therefore, the triangle ΔABC - is right.

 

3) Using the formula of the law of cosines

, we find the cosine of the angle B

Cos B = == -< 0.

Since the cosine of the angle B is less than zero, hence the angle B is obtuse, and the triangle ΔABC is obtuse.

***

 

The solving the triangle having used the angle between the sides

Problem 82.

Given:

the triangle ΔABC, two angles and the side

A = 45°

C = 30°

AD = 3 m

Find: the length of all sides of the triangle ΔABC = ?

Solution:

Knowing the size of two angles in the triangle ΔABC, we find the third angle B = 180° - (30° + 45°) = 105°

We find the angle DAB and consider ΔADC

DAB = 180° - (90° + 45 + 30°) = 15°

DAC = 15° + 45° = 60°

Using the law of sines

, we find the side AC

AC = (3 • 1) • 2 = 6 (m)

Using the law of sines

, we find the side AB

AB = ≈ 3 (m)

Using the law of sines

, we find the side BC

BC =≈ 4 (m)

Answer: AB ≈ 3 m, AC = 6 m, BC ≈ 4 m.

***

 

Problem 83.

Given:

the triangle ΔABC

three sides a = 14, b = 18,

c = 20

Find:

all the angles of the triangle ΔABC = ?

Solution:

Since the larger side lies against the larger angle, we see that using the formula of the law of cosines

Cos C =, we find the cosine of the angle C

Cos C = = ≈ 0.24

Using the calculation on the scientific calculator, we find the approximate value of the angle C

C ≈ 76°07’

Using the formula of the law of cosines

Cos B =, we find the cosine of the angle B

 

Cos B = ==≈ 0.4857

Using the calculation on the scientific calculator, we find the approximate value of the angle B

B ≈ 60.941 ≈ 60°57’

Therefore, A = 180° - (76°13’ + 60°57’) ≈ 42°56’

Answer: A ≈ 42°56’ ; B ≈ 60°57’ ; C ≈ 76°07’

***

Problem 84.

Given:

the triangle ΔEKP, the side and two angles

EP = 0.75

P = 40°

K = 25°

 

Find: the side of the triangle PK = ?

Solution:

Using the law of sines

, we find the side PK

E = 180° - (40° + 25°) =115°

Sin 115° = Sin (180° - 65°) = Sin 65°

Then

 

PK = ≈ 1.61

Answer: PK ≈ 1.61.

***

 

Problem 85.

Given:

the triangle ΔABC, two sides and the angle

b = 18, c = 12

A = 50°

 

Find: solve the triangle - determine the values of the side and two angles

(a, B, C ) = ?

Solution:

Using the formula of the law of cosines

, we obtain

a = = ≈ 13.8

Using the formula of the law of cosines

Cos C =, we find the cosine of the angle C

Cos C == ≈ 0.7457

Using the calculation on the scientific calculator, we find the approximate value of the angle C

C ≈ 41°47’

Therefore, B = 180° - (50° + 41°47’) ≈ 88°13’

Answer: a ≈ 13.8 ; B ≈ 88°13’ ; C ≈ 41°47’

***