The contents of this webpage:
Derivation of the formula for the circumference.
Let C and C′ - be the lengths of the circles with the radius R and R′. Let us inscribe the regular polygons in the circles.
Pn and Pn′ - are the perimeters of the regular polygons,
an and an′ are the sides of the regular polygons.
Pn = n • an = n • 2R • Sin![]()
Pn′ = n • an = n • 2R′ • Sin![]()
Then ![]()
Knowing that the perimeters Pn and Pn′ - are approximate values of the lengths of the circles C and C′, as n →∞, we obtain
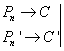
![]()
![]()
But by the equality ![]() we obtain
we obtain ![]()
By the property of the proportion ![]()
The value of the value of π (read "pi") is approximately 3.14.
![]()
![]()
Formula for the circumference:
![]()
***
If the radius R = 4, then the circumference C = 2πR = 2 • 3.14 • 4 = 25.12
If C = 82, then the radius of the circle R =![]() =
= ![]() = 13.1
= 13.1
If C = 18π, then the radius of the circle R =![]() =
= ![]() = 9
= 9
***
Given:
a is the side of the regular triangle
Find: the length of the circumscribed circle
Solution:
Since the side of a regular polygon
an = 2R • Sin (![]() ), then the side of the regular triangle
), then the side of the regular triangle
a = R![]()
![]() R =
R = ![]()
Then the length of the circle circumscribed about the regular triangle is C = 2πR = ![]()
***
Derivation of the formula for calculating the arc L with the degree measure α.

The degree measure of the circumference is 360°,
The circumference is C = 2πR
The arc length of 1° equals ![]()
Then the length of the arc of the circle in α degrees:

***
Given:
the radius R= 6 cm,
the angle of the arc
| 1) α = 30° | 2) α = 45° | 3) α = 60° | 4) α = 90° |
Find: the length of the arc of the circle
Solution:
1) L = ![]() • 30° =
• 30° = ![]() • 30° = π (cm)
• 30° = π (cm)
2) L = ![]() • 45° =
• 45° = ![]() • 3 = 1,5π (cm)
• 3 = 1,5π (cm)
3) L = ![]() • 60° = 2π (cm)
• 60° = 2π (cm)
4) L = ![]() • 90° = 3π (cm)
• 90° = 3π (cm)
***
Given:
ABCDEF is the regular hexagon,
the area of the hexagon S6 = 24![]() cm2
cm2
Find: what is the length of the circumscribed circle C = ?
Solution:
C = 2πR
Therefore, we need to find the radius of the circumscribed circle.
The area of the hexagon is determined by the formula
S6 =![]() • P6 • r6
• P6 • r6
The radius of the inscribed circle is determined by the formula
r6 = R • Cos ![]() =
= ![]() • R
• R
The side of the hexagon is equal to the radius of the circumscribed circle: a6 = R
Then the perimeter of the hexagon P6 = 6 • a6 = 6R (cm)
S6 =![]() • P6 • r6 =
• P6 • r6 = ![]() • 6R •
• 6R • ![]() • R = 1.5
• R = 1.5![]() •R2
•R2
24![]() = 1.5
= 1.5![]() •R2
•R2
R2 = ![]() = 16
= 16 ![]() We obtain the radius of the circumscribed circle
We obtain the radius of the circumscribed circle
R = ![]() = 4 (cm)
= 4 (cm)
Then the length of the circumscribed circle is
C = 2πR = 2π • 4 = 8π (cm)
Answer: 8π cm.
***
Given:
ABCD is the square,
the side of the square is AB = a
Find: the length of the inscribed circle C = 2π • r = ?
Solution:
r4 = R • Cos ![]() = R • Cos 45° =
= R • Cos 45° = ![]() R
R
C = 2π • r = 2π • ![]() R = π • R
R = π • R![]()
AB = a = 2r = R![]() . Therefore, C = π • R
. Therefore, C = π • R![]() = π • a
= π • a
Answer: the length of the circle inscribed in the square C = π • a
***
Given: the circle (O; R) is circumscribed about the following figures
1) Δ ABC is the inscribed right triangle;
a, b are the legs of the triangle
2) Δ ABC is the inscribed isosceles triangle;
a is the base, b is the side
3) ABCD is the inscribed rectangle,
BC = a is the side of the rectangle,
α is the acute angle between the diagonals
Find: the length of the circumscribed circle C = 2πR = ?
Solution:
1)
2R = AB ![]() R =
R = ![]() AB
AB

AB = ![]()
Then the length of the circle circumscribed about the right triangle
C = 2π • ![]() •
• ![]() = π
= π![]()
2)
BH = ![]() =
= ![]()

The area of the triangle is equal to half the product of the base by the height
SΔABC = ![]() BH • AC =
BH • AC = ![]() (1)
(1)
But the area of the triangle can also be found by dividing the product of its three sides by four radii of the circumscribed circle:
SΔABC = ![]() =
= ![]() (2)
(2)
Using equalities (1) and (2), we obtain
![]() =
=![]()
![]() R =
R = ![]()
Then the length of the circle circumscribed about an isosceles triangle
C = 2π •![]()

OB = OC = OA = OD = R
We draw OH is the height and the bisector of the isosceles triangle ΔAOD.
Consider the right triangle ΔOHD.
![]() AOD = 180° – α,
AOD = 180° – α,
![]() HOD =
HOD = ![]() • (180° – α)
• (180° – α)
![]() ODA = 180° –
ODA = 180° – ![]() DHO –
DHO – ![]() HOD
HOD
![]() ODA =
ODA =![]() OAD = 180° – 90° –
OAD = 180° – 90° – ![]() • (180° – α) =
• (180° – α) =![]()
AH = HD = ![]()
Cos![]() OAD = Cos
OAD = Cos![]() =
= ![]() =
= ![]()
![]()
R = 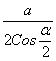
Then the length of the circle circumscribed about the rectangle
C = 2π • 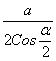 =
= ![]()
***
Given:
A1A2...An is the regular polygon
the circle (O; R)
the small circle′ (O; rn)
S is the area of the circle
Sn′ is the area of the small circle

S = πR2
Proof:
Consider a regular polygon (see the figure).
The area of the circle is larger than the area of the polygon:
Sn < Scircle
The area of the polygon is larger than the area of the small circle:
Sn′ < Sn
Then Sn′ < Sn < S (1)
The radius of a circle inscribed in the regular polygon
rn = R • Cos (![]() )
)
As n→∞ the cosine Cos (![]() )→1, therefore rn → R
)→1, therefore rn → R
Therefore, Sn′ → S as n→∞.
From inequality (1) it follows that Sn → S as n→∞.
We know that the area of a regular polygon
Sn = ![]() Pn • rn, where Pn is the perimeter of the polygon A1A2...An.
Pn • rn, where Pn is the perimeter of the polygon A1A2...An.
Knowing that rn → R, Pn → 2πR, Sn → S as n→∞.
Then S = ![]() Pn • rn =
Pn • rn = ![]() 2πR • R = πR2
2πR • R = πR2
Formula of the area of the circle:
![]()
***
Definition:
The sector of the circle or simply the sector is a part of the circle bounded by an arc and two radii connecting the ends of the arc to the center of the circle.

πR2 is the area of the circle.
If the measure of the circular sector is equal to 1°, then the area of this sector is equal to ![]()
If the measure of the circular sector is equal to α degrees, then the area of this sector is equal to ![]()
Formula of the sector of the circle:
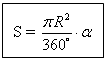 , where
, where
α is the degree measure of the arc.
***
Given:
![]() AOB = 72°
AOB = 72°
S is the area of the circular sector
Find: R is the radius of the circle
Solution:
S = ![]()
360° • S = πR2 • α
R2 = ![]() =
= ![]()
![]() R =
R = ![]()
Answer: the radius is R = ![]()
***
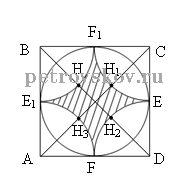
Given:
ABCD is the square,
the side of the square is AB = a
Calculate:
the area of the filled figure SEFE1F
1 = ?
Solution:
S = ![]()
Consider in the figure the sector FAE1H3, where AF = AH3 = R = ![]()
S = ![]()
![]() S1 =
S1 = ![]() • 90° =
• 90° = ![]()
The area of four sectors:
S1+2+3+4 = 4 • ![]() =
=![]()
The area of the square
SABCD = ![]() AC • BD.
AC • BD.
Consider ΔACD, where AD = CD = a.
By the Pythagorean theorem:
AC = ![]()
Then Sn= ![]()
![]() •
• ![]() = a2
= a2
Therefore, the area of the filled figure
SEFE1F
1 = SABCD – S 1+2+3+4 = a2 –
![]() =
= ![]()
Answer: ![]() .
.
***

Given:
the circle (O;OH1)
the circle (O;OH2)
the circle (O;OH3)
the circle (O;OH4)
OH1 = 1, OH2 = 2
OH3 = 3; OH4 = 4
Find: the area of the circle (O;OH1),
the area of each of the three targets = ?
Solution:
Scircle1 = πR2 = π • (OH1)2 = π • 1 = π
Scircle2 = πR2 = π • (OH2)2 = π • 4 = 4π
Scircle3 = πR2 = π • (OH3)2 = π • 9 = 9π
Scircle4 = πR2 = π • (OH4)2 = π • 16 = 16π
Starget2 = Scircle2 – Scircle1 = 4π – π = 3π
Starget3 = Scircle3 – Scircle2 = 9π – 4π = 5π
Starget4 = Scircle4 – Scircle3 = 16π – 9π = 7π
Answer: Scircle1 = π; Starget2 = 3π; Starget3 = 5π; Starget4 = 7π.
***
Given:
the circle (O;R), circumscribed about the quadrilateral and the triangle
1) ABCD is the rectangle,
a and b are the sides of the rectangle

a is the leg or the cathetus of the triangle,
α is the opposite angle
Find: the area of the circle shown in the figure.
S = πR2 = ?
Solution:
1)
BD = 2BO = 2R
Consider the right triangle ΔABD.
By the Pythagorean theorem:
BD2 = AB2 + AD2
(2R)2 = a2 + b2
R2 = ![]()

2)
Find the area of a circle having used its diameter AB = 2AO = R
Sin α = ![]()
![]() AB =
AB = ![]()
![]()
2R = ![]()
![]() R =
R = ![]()
Therefore,
S = πR2 = π • ![]() = π •
= π • ![]() =
=![]()
Answer: 1) π •![]() ; 2)
; 2) ![]() .
.
***
Given:
ΔABC is the right triangle
![]() circle1 (O1; AO1) on the hypotenuse AB
circle1 (O1; AO1) on the hypotenuse AB

![]() circle3(O3; CO3) on the leg AC
circle3(O3; CO3) on the leg AC
Prove:
The sum of the area of the semicircle on the hypotenuse is equal to the sum of the areas of the semicircles on the legs
S1 = S2 + S3
Proof:
Suppose that AB = c; AC = a; BC = b.
The formula of the area of the circle sector
S = ![]()
S = ![]() =
=![]()
S1 = ![]() • O1A2, where O1A =
• O1A2, where O1A = ![]() c
c ![]() S1 =
S1 =![]() •c2
•c2
S2 = ![]() • O2B2, where O2B =
• O2B2, where O2B = ![]() b
b ![]() S2 =
S2 =![]() •b2
•b2
S3 = ![]() • O3C2, where O3C =
• O3C2, where O3C = ![]() a
a ![]() S3 =
S3 =![]() •a2
•a2
Then S2 + S3 =![]() •a2 +
•a2 +![]() •b2 =
•b2 = ![]() • (a2 + b2)
• (a2 + b2)
By the Pythagorean theorem:
c2 = a2 + b2
Therefore,
S2 + S3 = ![]() • (a2 + b2) =
• (a2 + b2) = ![]() • c2 = S1
• c2 = S1
Therefore S1 = S2 + S3
***
Given:

AO is the radius
AO = 10 cm
![]() AMB =
AMB = ![]() AOB = 60°
AOB = 60°
Find:
what is the area of the circle sector with the arc ALB = ?
Solution:
The degree measure of the arc
![]() ALB = 360° – 60° = 300°
ALB = 360° – 60° = 300°
Then the area of the circle sector
S = ![]() =
= ![]() =
= ![]() ≈ 261.67 ≈ 262 (cm2)
≈ 261.67 ≈ 262 (cm2)
Answer: the area of the segment of the circle is S ≈ 262 cm2.
***
Given:
circle (O; OH) is inscribed in ΔABC
the triangle ΔABC is equilateral
AB = a

Find: what is the area of the circle
Scircle = ?
Solution:
S = πR2 = πr2
Consider the triangle ΔABH – is the right triangle.
AO is the bisector of the angle ![]() A.
A.
Therefore, ![]() OAH = 60° : 2 = 30°
OAH = 60° : 2 = 30°
OH = ![]() AO
AO
r = ![]()
![]() AOH = 180° – (30° + 90°) = 60°
AOH = 180° – (30° + 90°) = 60°
Sin 60° = ![]()
![]() the radius of the circumscribed circle R =
the radius of the circumscribed circle R = ![]()
Then the radius of the inscribed circle r = ![]() : 2 =
: 2 = ![]()
Therefore, the area of the circle S = πr2 = ![]() =
= ![]()
Answer: Scircle =![]()
***

Given:
the small circle (O; OD)
the area of a large circle
S circle(O; OC) = 314 mm2
the diameter of a small circle
D circle(O; OD) = 18.5 mm
Find: the difference in diameters
HC = ?
Solution:
S = πR2
314 = πR2
![]() =
= ![]() = 10 (mm)
= 10 (mm)
D2 = 2R = 2 • 9.25 = 18.5 (mm)
R2 = 9.25 mm
HC = R1 – R2 = 10 – 9.25 = 0.75 (mm).
Answer: 0.75 mm.
***
Given:
the small circle (O; OH) is the hole of the pipe
OH = 3m is the radius of a small pipe
AB = 1m is the difference in diameters between the two pipes

1 m2 → 0.8 dm3
Find: how much sand you need to fill the space between two pipes
Solution:
Consider the circle′ (O; OH).
The area of this circle:
S′ = πR2 = 9 • 3.14 ≈ 28.26 (m2)
Consider the circle′′ (O; OH+AB).
S′′ = πR2 = 16 • 3.14 ≈ 50.24 (m2)
Then the area between two pipes
S = S′′ – S′ = 50.24 – 28.26 ≈ 21.98 (m2)
Then the required amount of sand
21.98 • 0.8 ≈ 17.58 dm3 ≈ 17.6 dm3
Answer: ≈ 17.6 dm3.
***